final-exam
别的章节笔记有考试无关内容,请注意甄别
00 考试说明
往年考试题型 (仅供参考,卷面总分 100 分):
·填空题:~30 分,1 分/每个空
·单选题/多选题:~32 分,2 分/每道题
·简答题:~12 分,共 2 道题
·计算题:~10 分,共 2 道题
·分析题:~16 分,共 3 道题
中文出卷,中文答题,闭卷考试!
不用准备和使用计算器 (因为题型中没有需要使用计算器的题目)、不需准备草稿纸 (考卷中提供草稿纸)
历年各章的题型和分数分布:
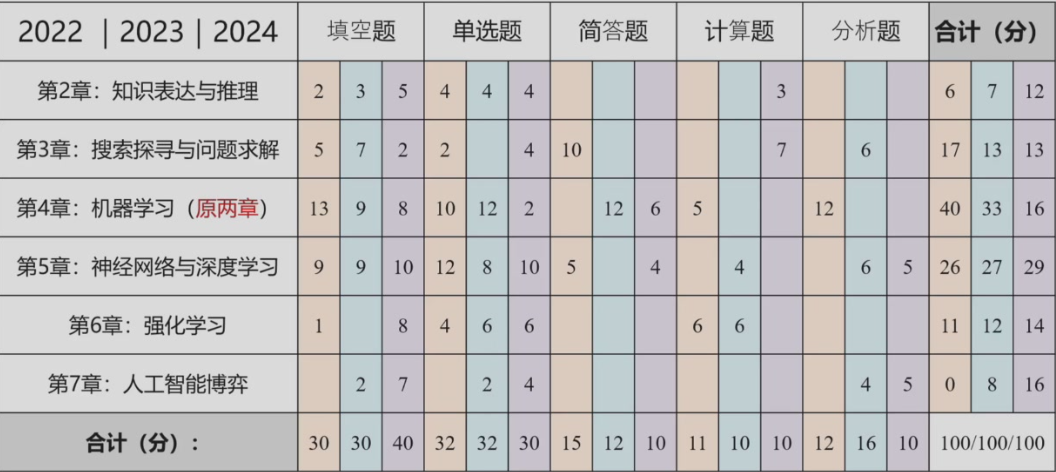
总体体验:
- 计院人工智能王东辉老师班课程体验:https://www.cc98.org/topic/5646555
复习准备:
- 大三下 cs 课程回忆与个人总结(AI 部分有讲到如何复习):https://www.cc98.org/topic/5643195
- 计院人工智能期末(关于如何复习):https://www.cc98.org/topic/5628179
资源和回忆卷:
- 2023-2024春夏 计院 人工智能 回忆卷 - CC98论坛
- 人工智能(计院)学习资源+2022-2023 学年回忆卷:https://www.cc98.org/topic/5635085
- 2021-2022 计院人工智能思维导图:https://www.cc98.org/topic/5353987
- 【资源】 2021-2022 春夏计院人工智能回忆卷:https://www.cc98.org/topic/5353848
01 知识表达与推理
- 代表性知识表达方法:命题逻辑、谓词逻辑、产生式规则(production rule)、框架 (frame) 表示法、知识图谱等
- 命题:确定为真或为假的陈述句
- 原子命题:不包含其他命题作为其组成部分的命题,又称简单命题
- 复合命题:包含其他命题作为其组成部分的命题
- 五种主要的命题联结词:与合取、或/析取、非/否定、条件/蕴含、双向条件/双向蕴含
- 逻辑等价:具有相同的真假结果,一般用 ≡ 来表示
- 逻辑推理是根据某种特定策略,从前提出发推出结论的过程。用符号 ⇒ 来表示推理过程,⇒ 的左侧表示推理的前提,⇒ 的右侧表示推理的结论
- 命题逻辑只能把复合命题分解为简单命题(即原子命题),无法对原子命题所包含的丰富语义(如个体、部分或全体等)进行刻画。因此,命题逻辑无法表达局部与整体、一般与个别的关系
- 谓词逻辑:刻画主体(个体和群体)之间逻辑关系的方法。在谓词逻辑中,将原子命题进一步细化,分解出个体、谓词和量词,来表达个体与总体的内在联系和数量关系,这就是谓词逻辑的研究内容
- 函数是从定义域到值域的映射;谓词是从定义域到二值集合 [True, False] 的映射。
- 全称量词和存在量词
- 知识图谱推理:作为归纳逻辑程序设计(inductive logic programming, ILP)的代表性方法,FOIL(First Order Inductive Learner,一阶归纳学习器)通过序贯覆盖学习推理规则。(FOIL 信息增益值(information gain)计算)
- 与 FOIL 算法不同,路径排序推理算法(PRA 的基本思想是将实体之间的关联路径作为特征,来学习目标关系的分类器。主要分为三步:特征抽取、特征计算、分类器训练
- 概率图模型:贝叶斯网络、马尔可夫网络、朴素贝叶斯模型、最大熵模型、隐马尔可夫模型、条件随机场、主题模型等
- 贝叶斯网络:用一个有向无环图来表示,其用有向边来表示节点和节点之间的单向概率依赖。贝叶斯网络满足局部马尔可夫性,即在给定一个节点的父节点的情况下,该父亲节点有条件地独立于它的非后代节点
- 马尔可夫网络:表示成一个无向图的网络结构,其用无向边来表示节点和节点之间的相互概率依赖。
- 马尔可夫逻辑网络是一种将概率图模型与一阶逻辑结合的工具,用于处理不确定性和复杂关系。它通过将一阶逻辑规则与权重结合,允许规则在不确定情况下灵活应用
- 克服辛普森悖论(Simpson’s Paradox):厘清真/假关联
- 关联关系的三种来源:因果关联(Causation)、混淆偏差(Confounding Bias)和选择偏差(Selection Bias)
- 因果分析的两种理论框架:潜在结果框架、结构因果模型
- 因果图的优势:易于计算变量的联合概率
- 因果推理:因果干预(改变明确存在关联关系的某变量取值,研究变量取值改变对结果变量的影响)与 do 算子(计算当系统中一个变量取值发生变化、其他变量保持不变时,系统输出结果是否变化)
被称为“因果效应差”(causal effect difference)或“平均因果效应”(average causal effect, ACE), 被称为因果效应。 - 反事实推理:某个事情已经发生了,则在相同环境中,这个事情不发生会带来怎样的新结果?
- 因果模型的层次化示意图
- 什么是逻辑:进行正确推理和充分论证的研究
- 符号主义人工智能 (symbolic AI) 就是脱胎于逻辑推理
逻辑关心的问题:
- 从前提出发,是否存在一个有效的论证或推理来支持所得到的结论
- 逻辑是一门研究推理的科学
- 逻辑和推理是人工智能的核心问题:通过归纳和演绎等手段对现有观测现象由果溯因 (归纳) 或由因溯果 (演绎)
规范化的逻辑知识:
- 人类认识世界的途径源于学习技能和解释已得知识
- 认知最重要的一种表现是分类
- 知识树/科学树 👉 对知识进行规范化描述
- 人类思想字母表 👉 按照规则组合,构造思想机器
知识表达方法
- 命题逻辑
- 谓词逻辑
- 产生式规则
- 框架表示法
- 知识图谱
- ...
1.1 命题逻辑
命题
命题:一个能确定为真或为假的陈述句
- 用小写符号来表示,如 p 或者 q
- 总有一个“值”,称为真值:为真 True 或为假 False
- 无法判断真假的描述性句子都不能作为命题

分类
- 原子命题:简单命题,不包含其他命题作为其组成部分的命题
- 符合命题:包含其他命题作为其组成部分的命题
- 可通过命题联结词 (connectives)对已有命题进行组合,得到新命题
| 命题连接符号 | 表示形式 | 意义 |
|---|---|---|
| 与 (and) | 命题合取 (conjunction),即“ |
|
| 或 (or) | 命题析取 (disjunction),即“ |
|
| 非(not) | 命题否定 (negation),即“非 |
|
| 条件 (conditional) | 命题蕴含 (implication),即“如果 |
|
| 双向条件 (bi-conditional) | 命题双向蕴含 (bi-implication),即“ |
逻辑等价:给定命题
| 逻辑等价的例子 | |
|---|---|
推理规则
推理是按照某种策略从前提出发推出结论的过程
- 用符号
来表示推理过程
| 推理规则的例子 | |
|---|---|
| 假言推理 (Modus Ponens) |
|
| 与消解 (And-Elimination) |
|
| 与导入 (And-Introduction) |
|
| 双重否定 (Double-Negation Elimination) | |
| 单项消解或单项归结 (Unit Resolution) | |
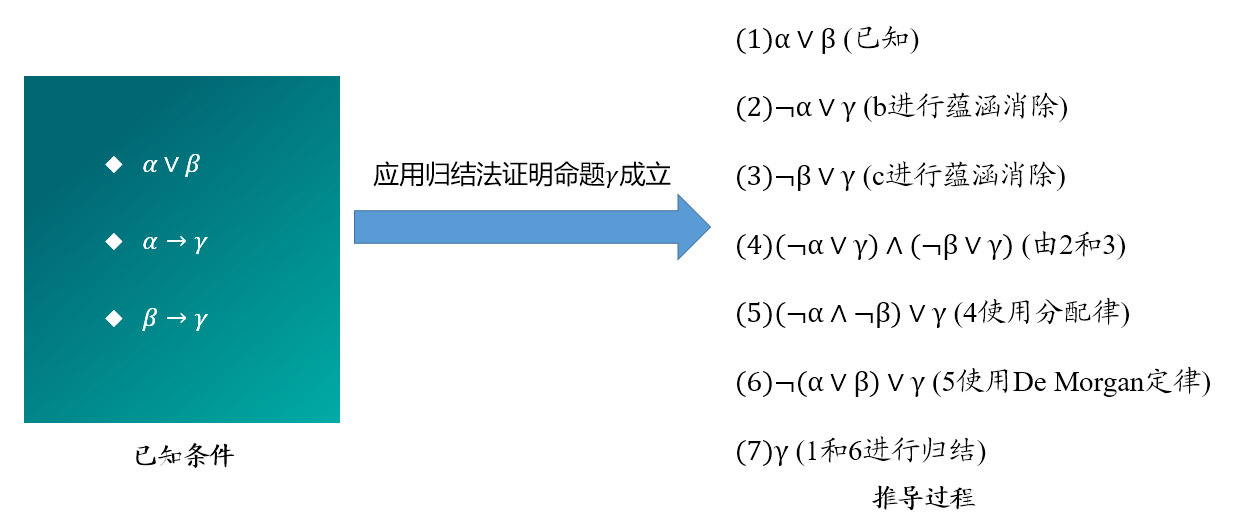
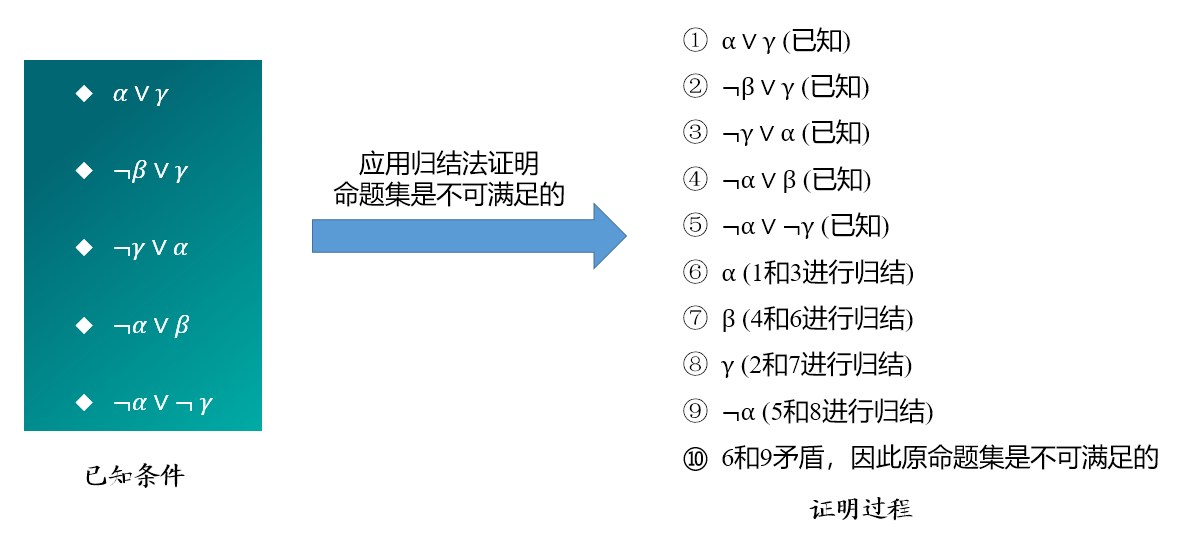
| 消解或归结 (Resolution) |
1.2 谓词逻辑
命题逻辑的局限性:在命题逻辑中,每个陈述句是最基本的单位 (即原子命题),无法对原子命题进行分解
- 不能表达局部与整体、一般与个别的关系
谓词逻辑:将原子命题进一步细化,分解出个体、谓词 predicate 和量词 quantifier
- 个体:所研究领域中可以独立存在的具体或抽象的概念
- 谓词:刻画个体属性或者描述个体之间关系存在性的元素,其值为真或为假
个体与谓词
例如,𝑃(𝑥) 表示:
- 𝑃是谓词, 𝑥是个体,𝑥被称为变量,其具体取值叫个体常项
- 函数是从定义域到值域的映射
- 谓词是从定义域到{True, False}的映射
- Richard 是国王。
- King (Richard)
- 其中,Richard 是一个个体常量,King 是一个描述“国王”这个一元关系的谓词
- Lucy 和 Lily 是姐妹
- Sister (Lucy, Lily)
- 其中,Lucy 和 Lily 是两个个体常量,Sitter 是一个描述“姐妹” 这个二元关系的谓词
量词
量词
- 全称量词 (universalquantifier, ∀)
- ∀𝑥表示定义域中的所有个体,∀𝑥𝑃(𝑥) 表示定义域中的所有个体具有性质 P
- 存在量词 (existentialquantifier, ∃)
- ∃𝑥表示定义域中存在一个或若干个个体,∃𝑥𝑃(𝑥) 表示定义域中存在一个个体或若干个体具有性质 P
量词之间的逻辑等价关系
变元
- 约束变元:在全称量词或存在量词的约束条件下的变量符号
- 自由变元:不受全称量词或存在量词约束的变量符号
相关的逻辑等价关系:
- A (x) 是包含变元 x 的公式,B 是不包含变元 x 的谓词公式
- A (x) 和 B (x) 是包含变元 x 的谓词公式
- 若多个量词都是全称量词或者都是存在量词,则量词的位置可以互换;若多个量词中既有全称量词又有存在量词,则量词的位置不可以随意互换
设 A (x, y) 是包含变元 x y 的谓词公式:
设
- 全称量词消去 (Universal Instantiation, UI):
- 全称量词引入 (Universal Generalization, UG)
- 存在量词消去 (Existential Instantiation, EI):
- 存在量词引入 (Existential Generalization, EG):
例 2.12 已知:
试证明:(
证明过程:
(已知) (已知) (2 的 EI) (1 的 UI) (由 3 知) (4 和 5 的假言推理) (由 3 知) (由 6 知) (7 和 8 的合取) (9 的 EG)
例 2.14 前提:1) 每驾飞机或者停在地面或者飞在天空;2) 并非每驾飞机都飞在天空
结论:有些飞机停在地面
形式化:plane
已知:
请证明:(
证明:
von_fly (已知) V on_fly von_fly
1.3 知识图谱推理
基本概念
知识图谱
- 由有向图构成
- 每个节点是一个实体,如人名、地名、事件和活动等
- 任意两个节点之间的边表示这两个节点之间存在的关系
- 任意两个相连节点及其连接边表示成一个三元组(triplet), 即 (left_node, relation, right_node)
- 也可以表示为一阶逻辑 (first order logic, FOL) 的形式
relation (left_node, right_node)
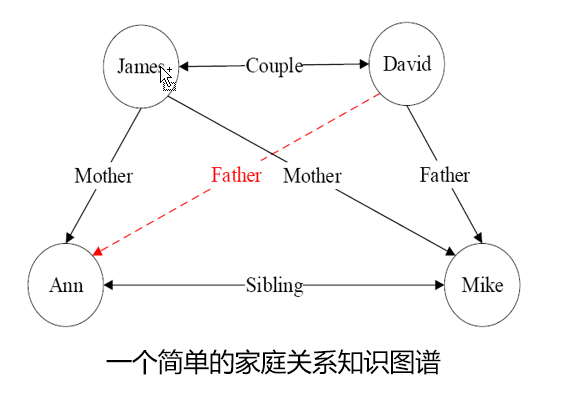
- 也可以表示为一阶逻辑 (first order logic, FOL) 的形式
关系推理是统计关系学习研究的基本问题:从现有知识发掘新的知识
现在面临一个问题,如何从知识图谱中推理得到:father (David, Ann) ?
- 从具体例子中学习如下规则
归纳逻辑程序设计 (inductive logic programming,ILP) 算法
ILP:使用一阶谓词逻辑进行知识表示,通过修改和扩充逻辑表达式对现有知识归纳,完成推理任务
- 代表性方法:一阶归纳学习 FOIL(First Order Inductive Learner)
- 通过序贯覆盖实现规则推理
对于:
- 前提约束谓词:我们通过学习得到
- 目标谓词:已知
- 输入:目标谓词 P, P 的训练样例(正例集合 E+和反例集合 E-),其他背景知识
- 输出:推导得到目标谓词
的推理规则
- 流程
- 将目标谓词作为所学习推理规则的结论
- 将其他谓词逐一作为前提约束谓词加入推理规则,计算所得到推理规则的 FOIL 信息增益值,选取最优前提约束谓词以生成新推理规则,并将训练样例集合中与该推理规则不符的样例去掉
- 重复 2 过程,直到所得到的推理规则不覆盖任意反例
从一般到特殊,逐步添加目标谓词的前提约束谓词,直到所构成的推理规则不覆盖任何反例
- 从一般到特殊指的是对目标谓词或前提约束谓词中的变量赋予具体值,如将
- 这一推理规则中目标谓词 Father (x, y) 所包含的 x 和 y 分别赋值为 David 和 Ann,进而进行推理
哪些谓词好呢? 可以作为目标谓词的前提约束谓词?
- 通过 FOIL 中的信息增益值来衡量
- 其中,
和 是增加前提约束谓词后所得新推理规则覆盖的正例和反例的数量, 和 是原推理规则所覆盖的正例和反例数量
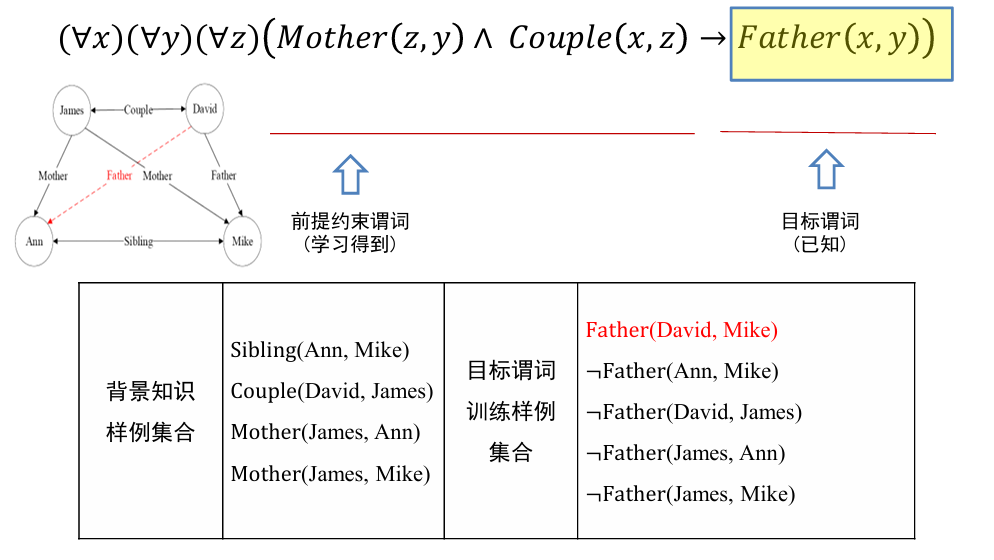
给定目标谓词,此时推理规则中只有目标谓词:
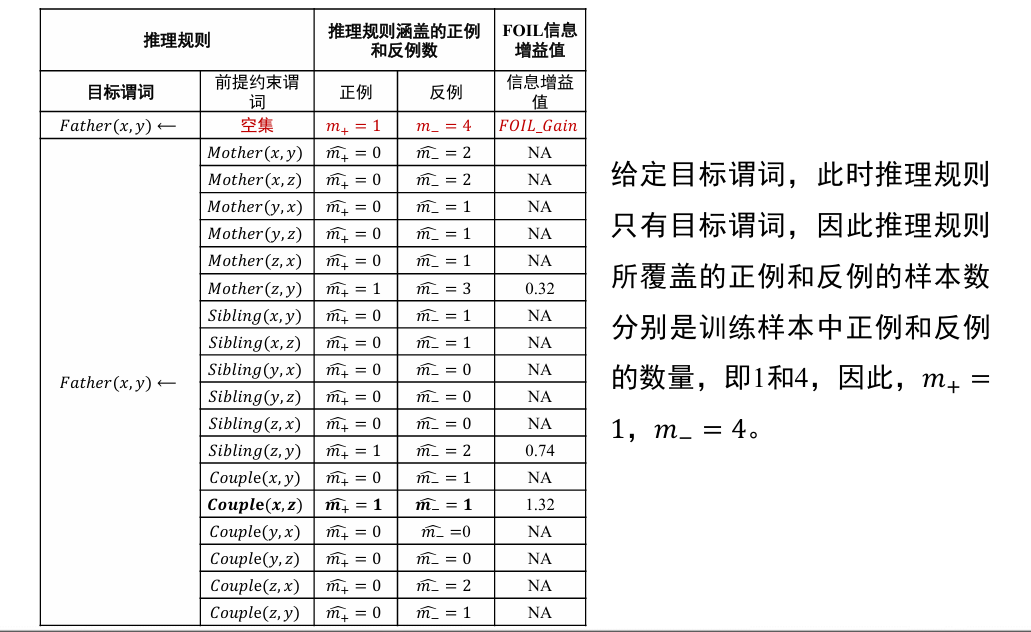
添加新的推理规则:
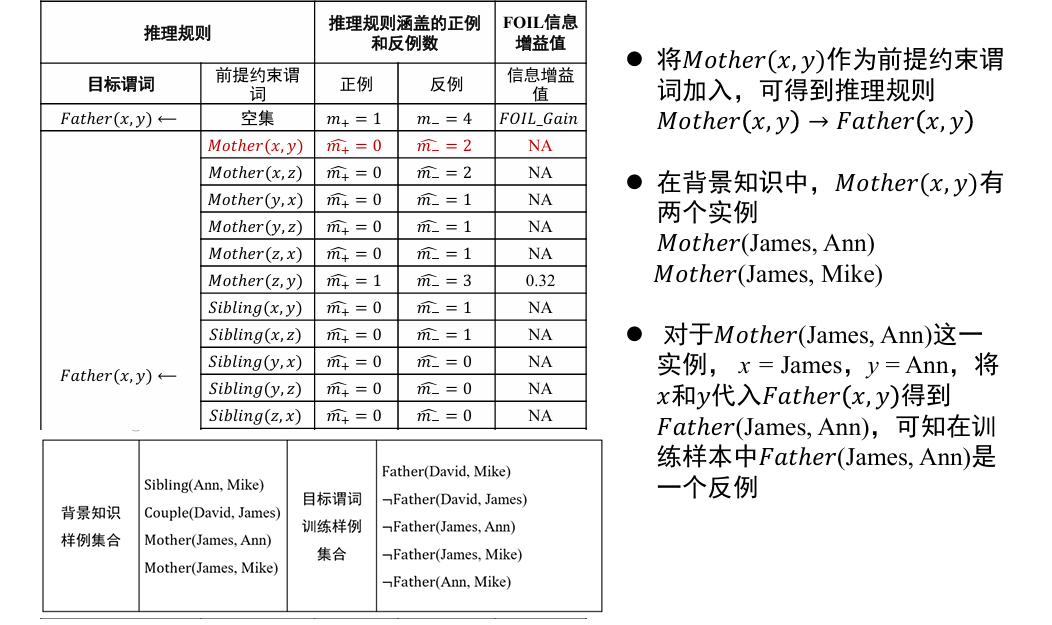
计算信息增益值:这里是 NA,说明这个规则不太好
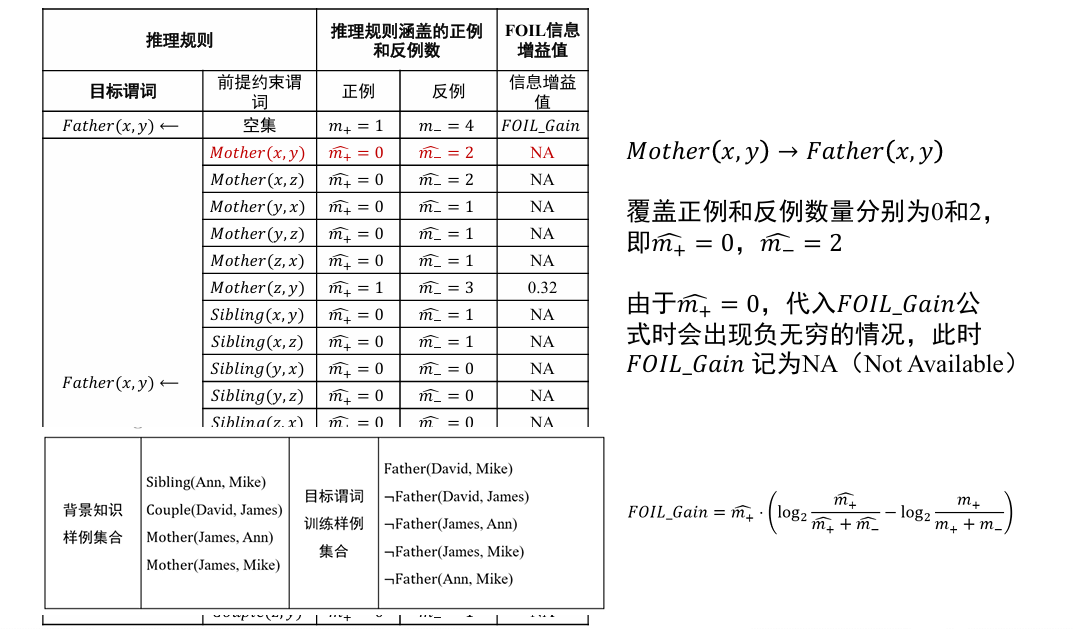
更换新的推理规则:
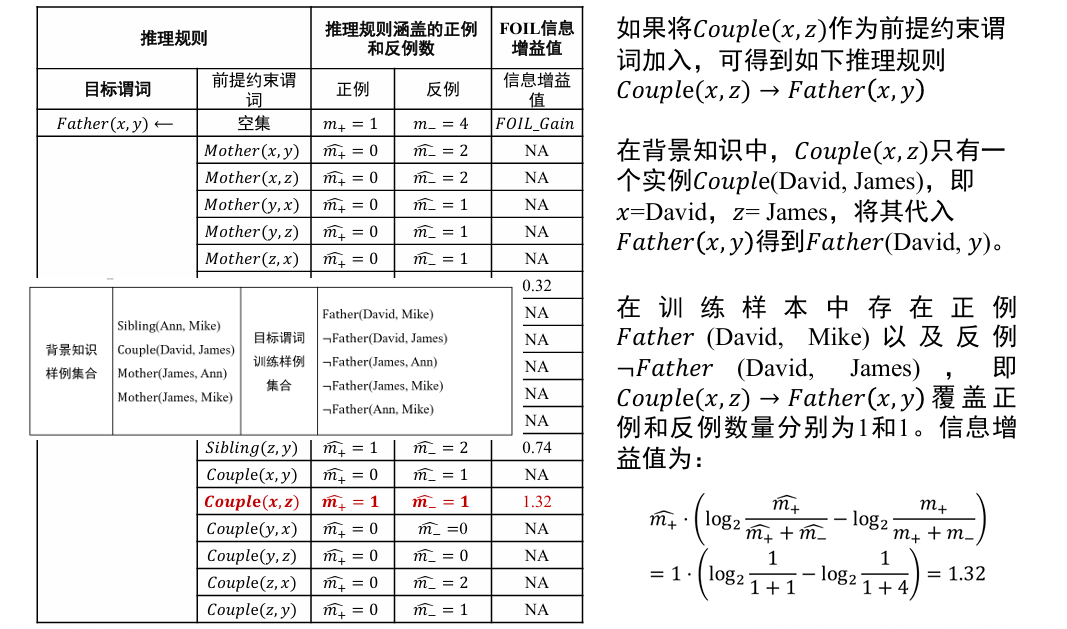
采用新推理规则:去掉不符合新推理规则的实例

添加新推理规则:此时不覆盖任何反例,算法结束
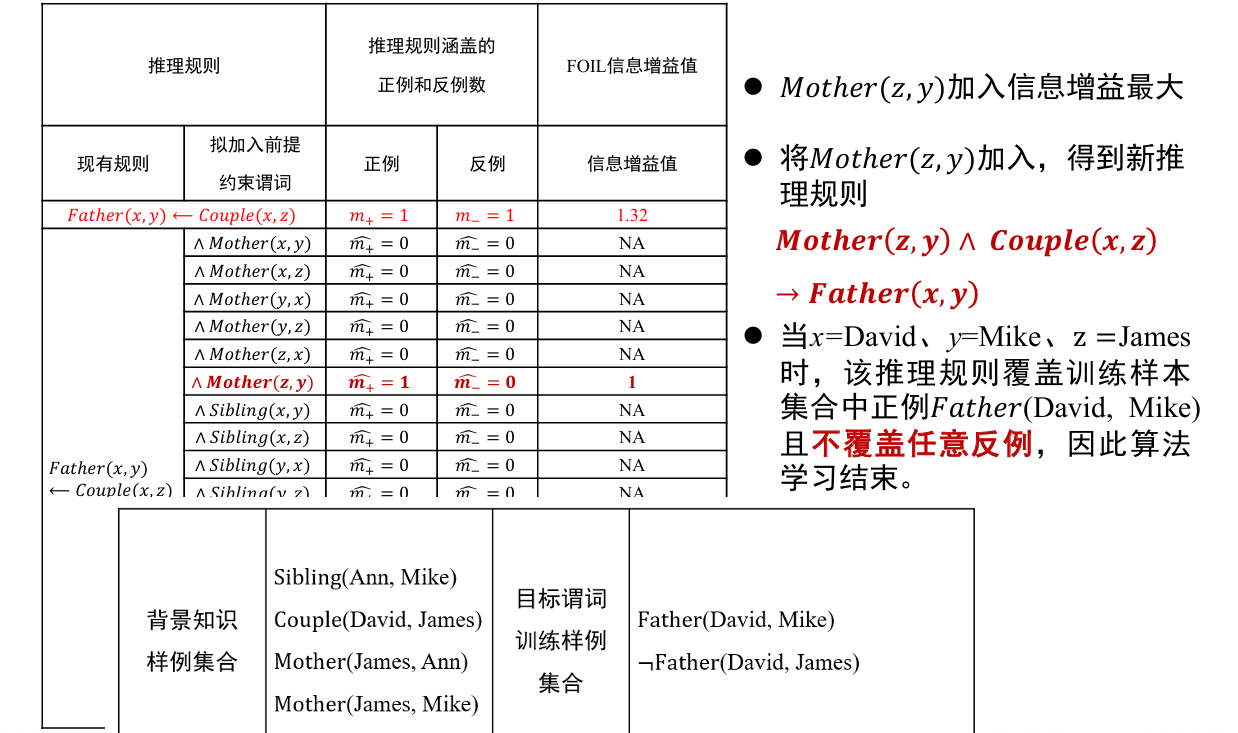
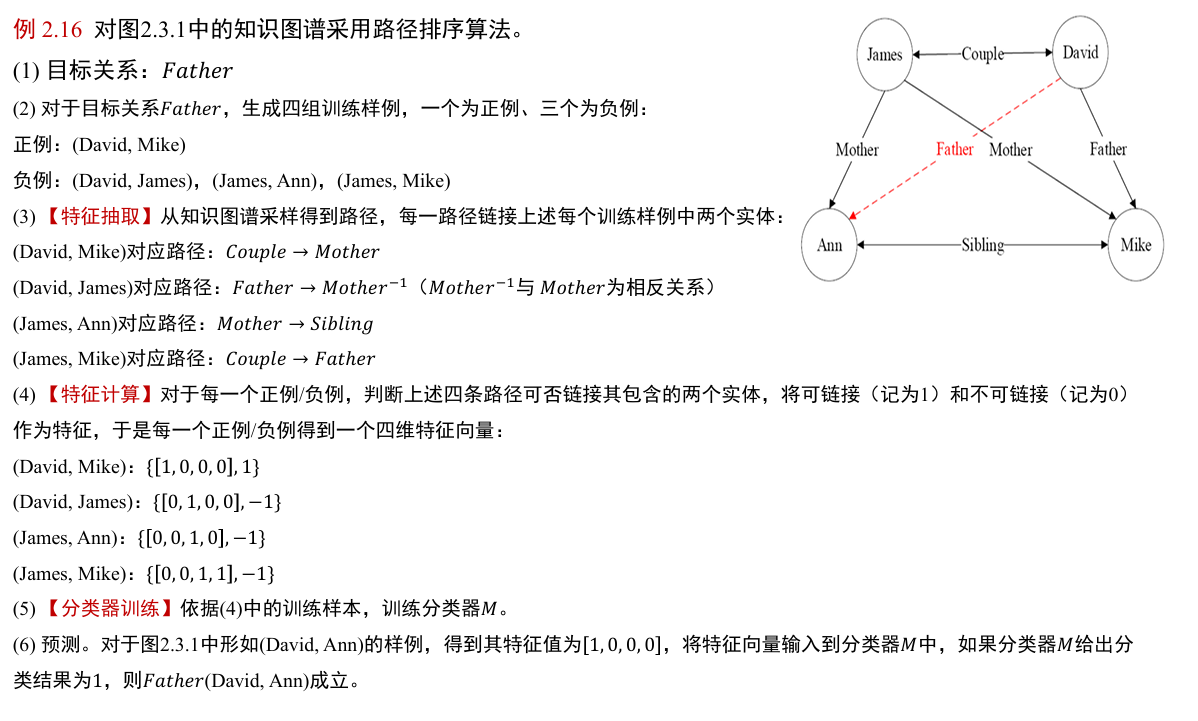
路径排序算法(path ranking algorithm, PRA)
路径排序推理算法(PRA)的基本思想:将实体之间的关联路径作为特征,来学习目标关系的分类器
可以分为如下三步:
- 特征抽取:生成并选择路径特征
的集合 - 生成路径的方式有随机游走 (random walk)、广度优先搜索、深度优先搜索等
- 特征计算:计算每个训练样例的特征值
- 特征值表示从实体节点 s 出发,通过关系路径
到达实体节点 的概率 - 也可以表示为布尔值,表示实体 s 到实体
之间是否存在路径 - 还可以是实体 s 和实体
之间路径出现频次、频率等
- 特征值表示从实体节点 s 出发,通过关系路径
- 分类器训练:根据训练样例的特征值,为目标关系训练分类器。当训练好分类器后,即可将该分类器用于推理两个实体之间是否存在目标关系
1.4 概率图谱推理
概率图(probabilistic graph)
- 如果两个节点之间存在连边,则可视为这两个节点之间具有概率依赖关系而相互影响
- 在这类图中,可用概率描述两个相连节点之间的关联,而不是假设节点之间的影响一定会百分之百发生。
- 基于概率图进行的推理被称为概率推理
概率图模型一般分为贝叶斯网络(Bayesian Network)和马尔可夫网络(Markov Network)两大类
- 贝叶斯网络
- 用一个有向无环图(directed acyclic graph)来表示,其用有向边来表示节点和节点之间的单向概率依赖
- 马尔可夫网络
- 表示成一个无向图的网络结构,其用无向边来表示节点和节点之间的相互概率依赖
贝叶斯网络
贝叶斯网络满足局部马尔可夫性(local Markov property):在给定一个节点的父节点的情况下,该父亲节点有条件地独立于它的非后代节点(non-descendant)
例如,对于如下网络:
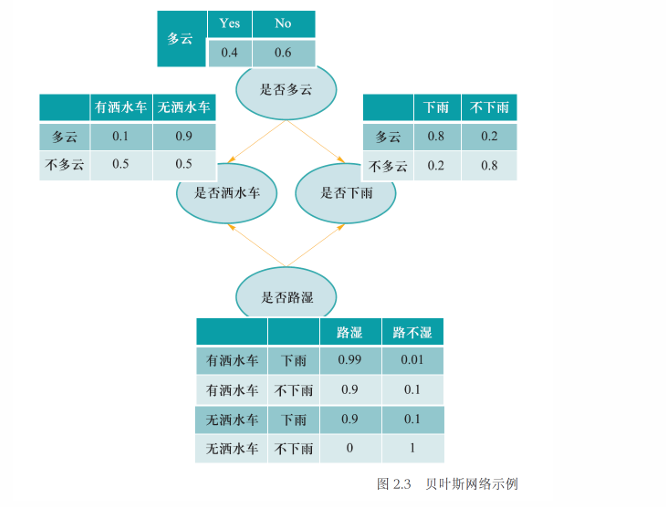
我们有:

马尔可夫逻辑网络
从概率统计的角度:
- 简明描述马尔可夫网中所存在的信息之间的关联
- 引入谓词逻辑,融入结构化知识
从一阶谓词逻辑角度:
- 添加不确定性 👉 对严格推理进行松绑
马尔可夫逻辑网络是一种将概率图模型与一阶逻辑结合的工具
给定一个由若干规则构成的集合,集合中每条推理规则赋予一定权重,则可如下计算某个断言 x 成立的概率:
其中
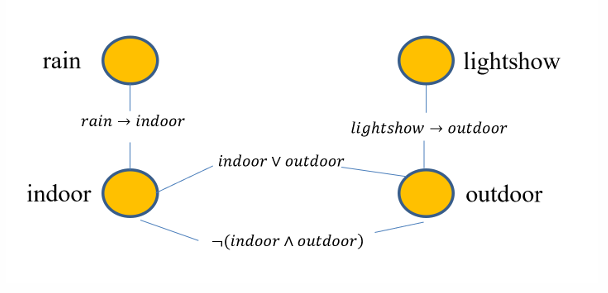
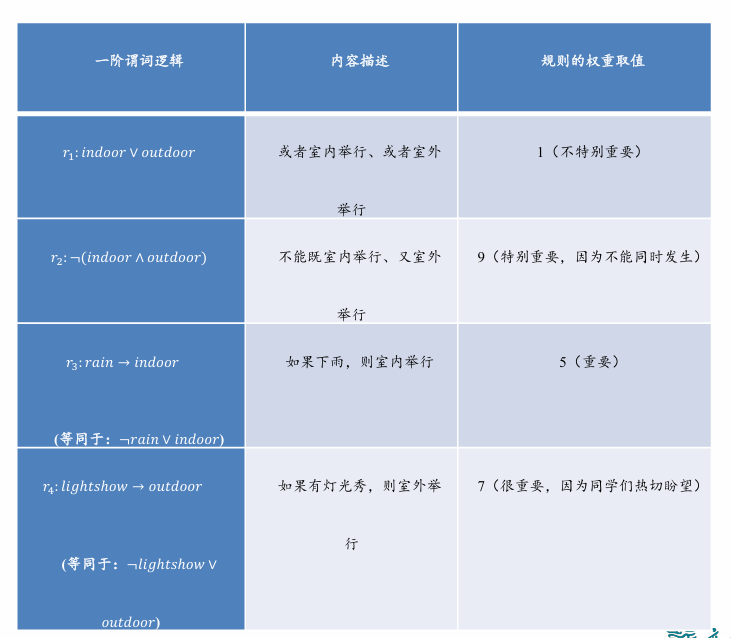
规则为真就取 1,否则取 0

1.5 因果推理
如下是某组病人在是否尝试新药以后的恢复情况:不用药病人的恢复率高于用药病人的恢复率
对所有病人按照性别分组后,当比较按性别分组的两类病人的恢复率时,却发现用药病人的恢复率均高于不用药病人的恢复率
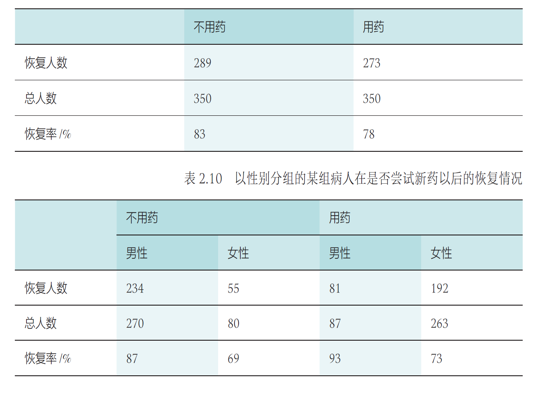
在某些情况下,忽略潜在的“第三个变量”(本例中性别就是用药与否和恢复率之外的第三个变量),可能会改变已有的结论
事实上,辛普森悖论的主要原因是因为“第三变量”导致了用药与否和恢复率之间的虚假关联
关联关系的三种来源
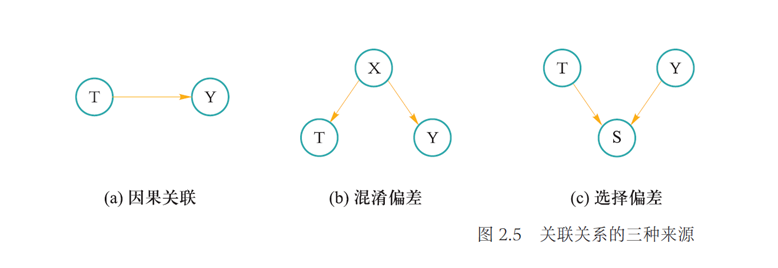
因果关联:数据中两个变量,如一个变量是另一个变量的原因,则该两变量之间存在因果关联
- 如图 (a) 所示,变量 T 是变量 Y 的原因
- "下雨会导致地面湿"
混淆关联:数据中待研究的两个变量之间存在共同的原因变量
- 如图 (b) 所示,变量 T 和 Y 存在共同的原因变量 X,即 X 是 T 的原因,同时也是 Y 的原因
- 如果忽略掉 X,那么 T 和 Y 在数据中会存在虚假关联
- "辛普森悖论":性别 (X) 会影响到患者吃药与否 (T) 以及其恢复率 (Y),如果我们忽略了性别,那么吃药与否和恢复率之间的关系就存在混淆关联
选择关联:数据中待研究的两个变量之间存在共同的结果变量
- 如图 (c) 所示,变量 T 和 Y 存在共同的结果变量 S,即 T 是 S 的原因,Y 也是 S 的原因
- 如果我们基于特定 S 的取值来选择一部分变量进行研究,那么 T 和 Y 在数据中就会存在虚假关联
- "X: 草地,Y: 狗的特征,S: 收集的图片是狗在草地上 👉 选择大量狗在草地上的图片,草地和狗就变得相关了"
两种理论框架
潜在因果框架
结构因果模型
- 因果图:有向无环图 👉 描述变量联合分布或者数据生成机制 👉 贝叶斯网络
对于有向无环图模型,模型中 d 个变量的联合概率分布:
表示节点 的父节点集合 (可以为空) - 跟前面讲贝叶斯网络时,提到的公式是一样的
例如,对于一个简单的链式图 (即有向无环图), 其联合概率分布可直接写成:
更复杂的,对于下图,有:
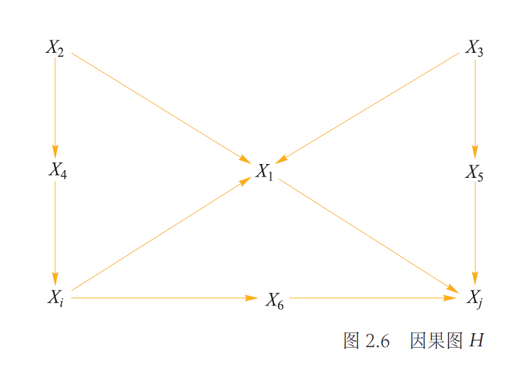
因果干预与 do 算子
干预:改变明确存在关联关系的某变量取值,研究变量取值改变对结果变量的影响
- "在已知商品价格和销售量存在关联关系的情况下,将商品价格提高一倍后,研究销售量会发生怎样的变化?"
"do"算子:计算当系统中一个变量取值发生变化、其他变量保持不变时,系统输出结果是否变化
表示的是当发现 时, 的概率;反映的是在取值为 的个体 上, 的总体分布 表示的是对 进行干预,固定其值为 时, 的概率;反映的是如果将每一个 取值都固定为 时, 的总体分布
因果效应
因果效应:给定因果图 G,PA 表示 X 的父节点集合,则
其中,z 是 PA 的具体取值
我们解释如上公式
以前面所言辛普森悖论为例,其因果图可以用下图表示:
- X 表示用药情况
- Y 表示病人的回复情况
- Z 表示性别
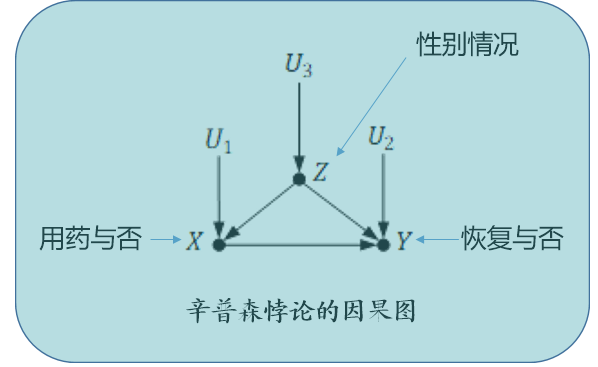
可以对病人的用药情况进行干预,来计算因果效应差:
对用药情况
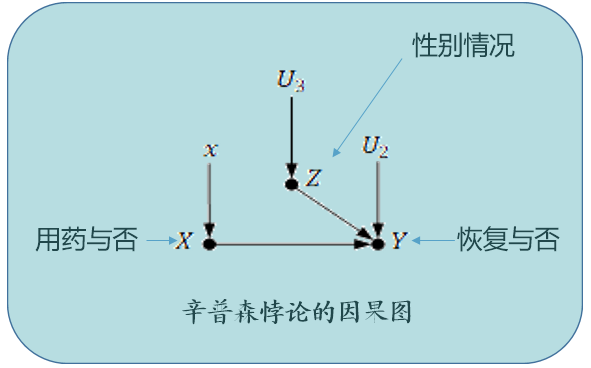
因果效应
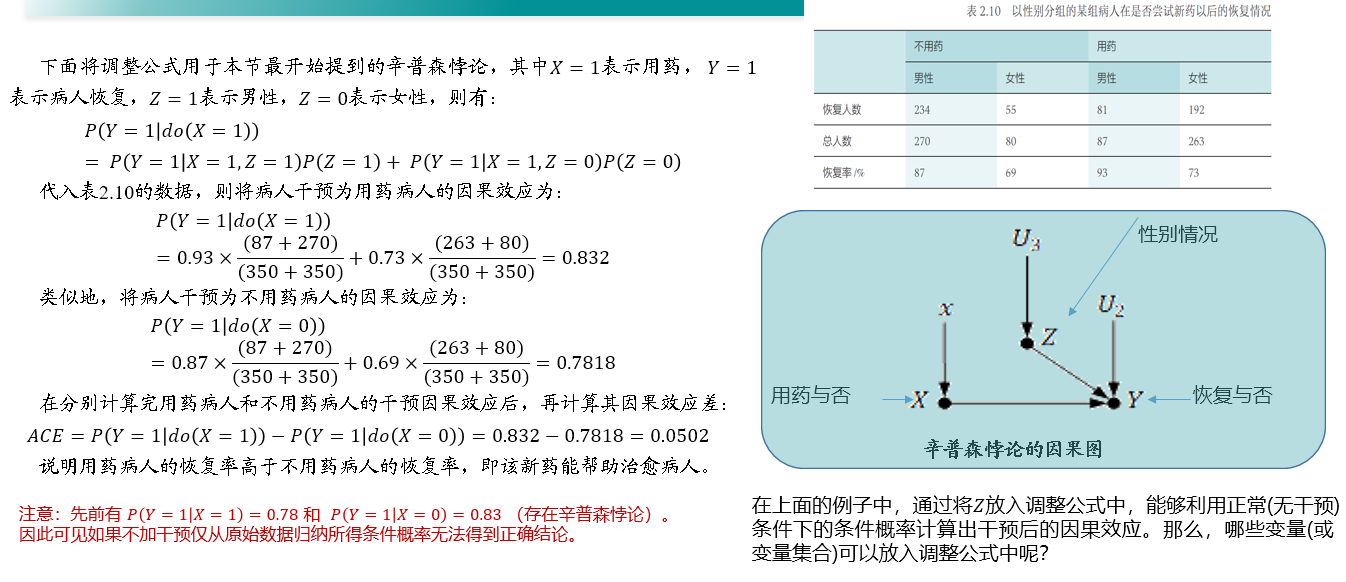
最后得到正常 (无干预) 条件下的概率表示的因果效应:
- 边缘概率
不随干预而变化,因为 Z 的取值不会因为去掉从 Z 到 X 的箭头而变化 - 条件概率
不变,因为 Y 关于 X 和 Z 的函数 并未改变 - 可用正常 (无干预) 条件下的条件概率来计算干预后的条件概率
- "调整公式" "Z 调整"
因果模型的层次化示意图
| 层次化示意图 | |||
|---|---|---|---|
| 可观测问题 | What if we see A (what is?) | $P(y\ | A)$ |
| 决策行动问题 | What if we do A (what if?) | $P(y\ | do (A))$ (如果采取 A 行为,则 y 将如何) |
| 反事实问题 | What if we did things differently (why) | $P(y'\ | A)$ (如果 A 为真,则 y′将如何) |
02 搜索探寻与问题求解
- 搜索的形式化描述:〈状态、动作、状态转移、路径/代价、目标测试〉
- 搜索过程可视为搜索树的构建过程:TreeSearch, GraphSearch
- 搜索算法的评测标准:完备性、最优性、时间复杂度、空间复杂度
- 放弃扩展部分结点的做法被称为剪枝(pruning),其对应的搜索算法被称为剪枝搜索
- 无信息搜索 vs 有信息搜索 / 启发式搜索
- 路径代价函数 g (n),评价函数 f (n)、启发函数 h (n)
- 贪婪最佳优先搜索 (Greedy best-first search):将启发函数作为评价函数的搜索过程,f (n) = h (n)
- A*搜索算法:评价函数和启发函数各司其职,f (n) = g (n) + h (n)
- A*算法的完备性和最优性取决于搜索问题和启发函数的性质(可容性、一致性,一致性必然导致可容性)
- 可容性: h (n) ≤ h*(n),如果启发函数是可容的,那么 A*算法满足最优性
- 一致性: h (n) ≤ c (n, a, n') + h (n'),满足一致性条件的启发函数一定满足可容性条件
- A*算法满足完备性的条件:
- a) 搜索树中分支数量是有限的,即每个结点的后继结点数量是有限的
- b) 单步代价的下界是一个正数
- c) 启发函数有下界
2.1 搜索算法基础
形式化描述
状态、动作、状态转移、路径/代价、目标测试
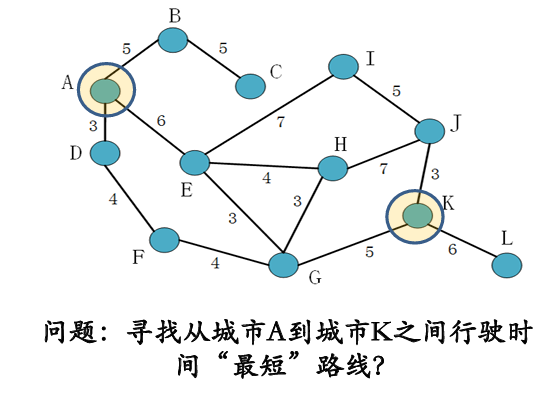
- 状态:对智能体和环境当前情形的描述
- 在最短路径问题中,每个城市即为一个状态
- 刚开始所在状态 (图中为 A ) 称为初始状态
- 完成任务时所在的状态 (图中为 K ) 称为终止状态
- 动作:从当前时刻所处状态转移到下一时刻所处状态所进行操作
- 状态转移:智能体选择了一个动作之后,其所处状态的相应变化
- 有边的两点之间才能转移
- 路径/代价:一个状态序列
- 状态序列被一系列动作所连接,如从 A 到 K 所形成的路径
- 单步代价:状态序列长度为 2
- 目标测试:评估当前状态是否为所求解的目标状态
我们用一棵树来记录算法探索过的路径
- 在搜索树中,同一个标号一定表示相同的状态
- 但是一个标号可能有多个的结点与之对应,即不同的节点对应了从初始状态出发的不同路径
搜索算法可以被看成是一个构建搜索树的过程,从根结点(初始状态)开始,不断展开每个结点的后继结点,直到某个结点通过了目标测试
搜索算法具备如下的评价指标:
- 完备性和最优性:解的质量、找到解的能力
- 时间复杂度和空间复杂度:算法的资源消耗
| 评价指标 | |
|---|---|
| 完备性 | 当问题存在解时,算法是否能保证找到一个解 |
| 最优性 | 搜索算法是否能保证找到的第一个解是最优解 |
| 时间复杂度 | 找到一个解所需时间 (通过拓展的节点数量来衡量) |
| 空间复杂度 | 在算法的运行过程中需要消耗的内存量 (通过算法同时记录的节点数量来衡量) |
而在搜索树中,我们通常使用如下变量,估计复杂度:
| 符号 | 含义 |
|---|---|
| 分支因子,即搜索树中每个节点最大的分支数目 | |
| 根节点到最浅的目标结点的路径长度 | |
| 搜索树中路径的最大可能长度 | |
| 状态空间中状态的数量 |
搜索算法框架
树搜索
边缘 (fringe) 集合: 集合ℱ用于保存搜索树中可用于下一步探索的所有候选结点,也叫做开表 (openlist)
- 输入:节点选择函数 (决定拓展顺序) pick_from,后继节点计算函数 (决定待拓展节点) successor_nodes
- 输出:从初始状态到终止状态的路径
- 算法流程
剪枝搜索
树搜索算法存在问题:并不是其所有的后继节点都值得被探索
- 在某些情况下,主动放弃一些后继结点能够提高搜索效率而不会影响最终搜索结果,甚至能解决无限循环(即算法不停机)问题
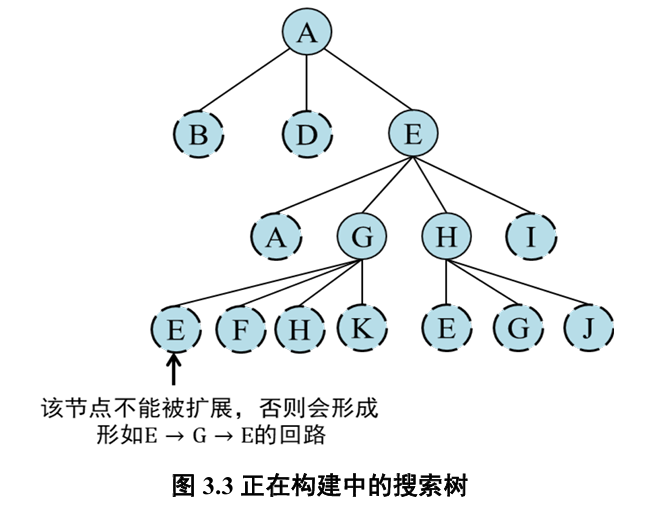
图搜索
在图搜索策略下,在边缘集合中所有产生环路的节点都要被剪枝,但不会排除所有潜在的可行解。因此在状态数量有限情况下,采用图搜索策略的算法也是完备的
- 输入:节点选择函数 pick_from,后继节点计算函数 successor_nodes
- 输出:从初始状态到终止状态的路径
- 算法流程
C 用于标记已经访问过的节点 - while F ≠
do - n ← pick_from (F)
- F ← F =
- if goal_test (n) then
- return n.path
- end
- if n.state
C then (删除引起环路的节点) - C ← C
- F ← F
successor_nodes (n)
- C ← C
- end
- end
2.2 启发式搜索 (有信息搜索)
| 辅助信息 | 所求解问题之外、与所求解问题相关的特定信息或知识。 | |
|---|---|---|
| 评价函数(evaluation function)f (n) | 从当前节点 n 出发,根据评价函数来选择后续结点 | 下一个结点是谁? |
| 启发函数(heuristic function)h (n) | 计算从结点 n 到目标结点之间所形成路径的最小代价值,这里将两点之间的直线距离作为启发函数 | 完成任务还需要多少代价? |
贪婪最佳优先搜索
评价函数
如下图所示
最小,选择 E 最小,选择 H - 以此类推...
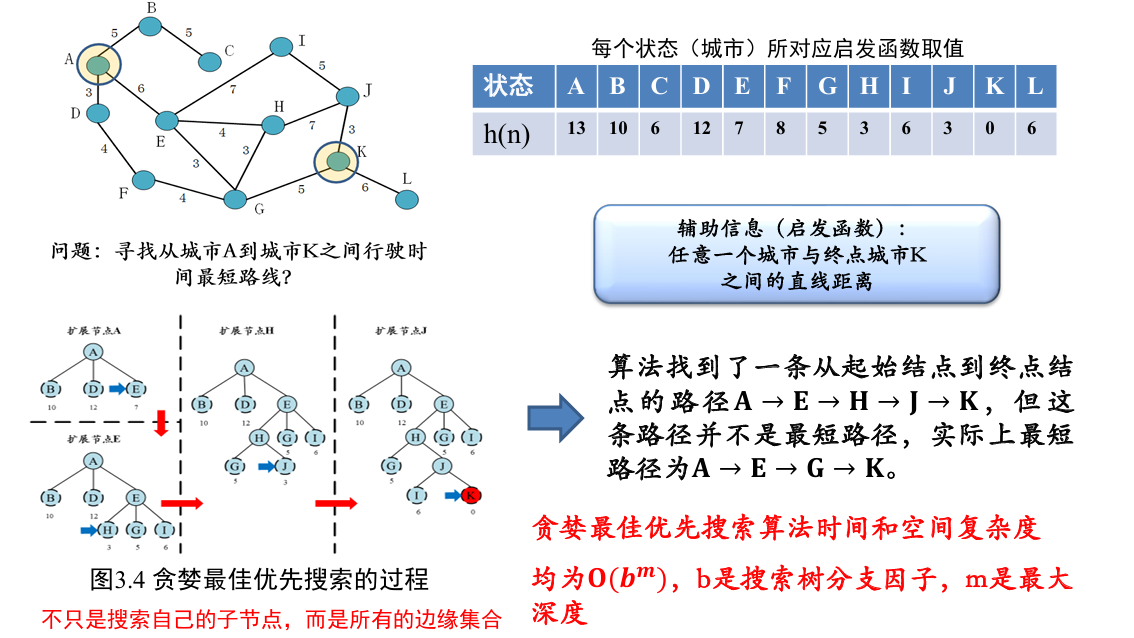
贪婪最佳优先搜索采用了排除环路的剪枝算法,但未考虑从初始节点到达该节点所需的代价
A* 算法
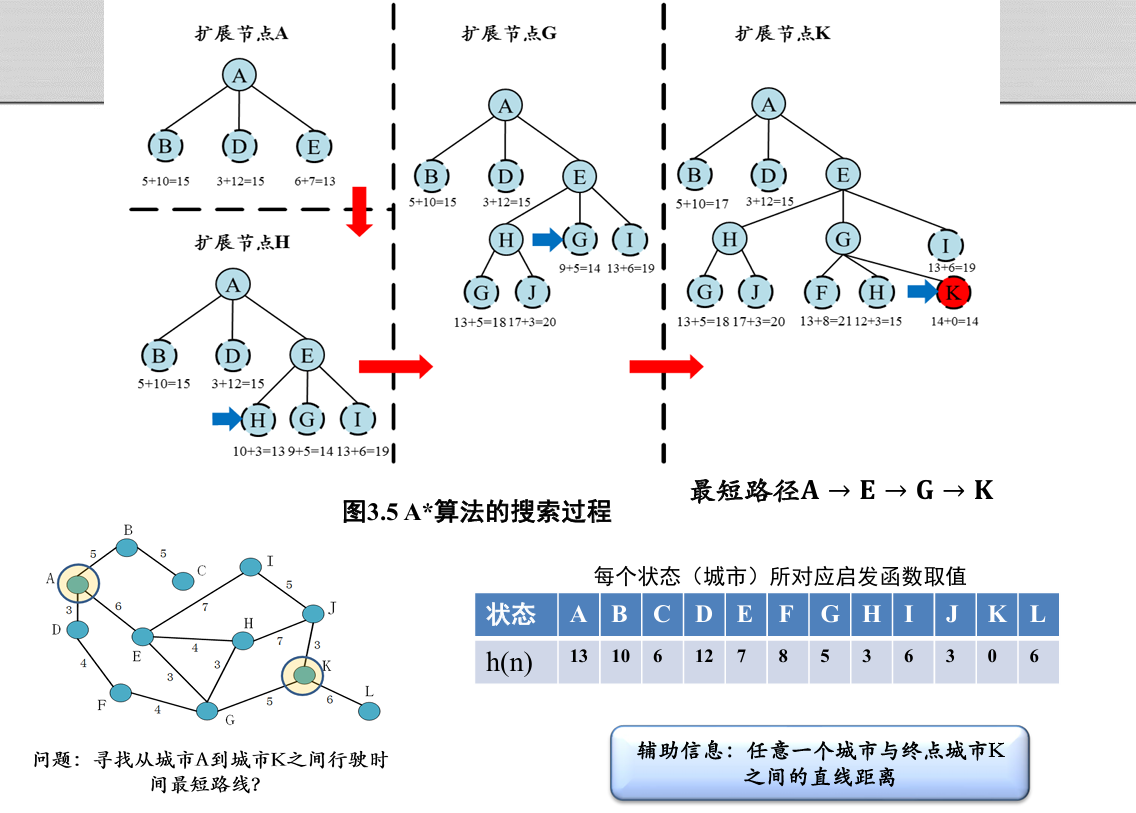
性能分析
| 符号 | 含义 |
|---|---|
| 节点 |
|
| 从起始节点到节点 |
|
| 节点 |
|
| 从节点 |
|
| 从节点 |
|
| 一个良好的启发函数需要满足如下两种性质: |
- 可容性 (admissible): 对于任意结点
, 有 , 如果 是目标结点,则有 是从结点 出发到达终止结点所付出的(实际)最小代价 - 即估计代价 ≤ 实际代价
- 一致性 (consistency): 启发函数的一致性指满足条件
- 三角不等式原则
- 在一些常见的搜索问题中,状态数量是有限的,此时图搜索 A*算法和排除环路的树搜索 A*均是完备的,即一定能够找到一个解
- 在更普遍的情况下,如果所求解问题和启发函数满足以下条件,则 A*算法是完备的
- 搜索树中分支数量是有限的,即每个节点的后继结点数量是有限的
- 单步代价的下界是一个正数
- 启发函数有下界
启发函数满足可容性时,假设树搜索的 A*算法找到的第一个终止结点为
对于此时边缘集合中任意结点
由于 A*算法对评价函数定义为
此时扩展其他任何一个边缘结点都不可能找到比结点
最优性,对于任意一个状态𝑡,它第一次被加入搜索树时的路径必然是最短路径
因为存在环路:如果有多个结点对应同一个状态 (即存在多条到达同一个城市的路径), 图搜索算法只会扩展其中的一个结点,而剪枝其余的结点
解决方案
- 方法 1:当算法从不同路径扩展同一结点时,不保留最先探索的那条路径,而是保留代价最小的那条路径
- 方法 2:要求启发函数满足一致性
- 由于图中存在环路,所以
并不总是成立 - 当启发函数满足一致性时,若结点𝑛′是结点𝑛的后继节点,则有
成立 - 假设状态𝑡加入搜索树时对应的结点为𝑛,在结点𝑛被加入搜索树后,若对应状态𝑡的任何结点𝑛′出现在边缘集合中,那么必然有𝑔(𝑛)≤𝑔(𝑛′)
- 由于图中存在环路,所以
2.3 对抗搜索
对抗搜索 (Adversarial Search) 也称为博弈搜索 (Game Search)
智能体 (agents) 之间通过竞争实现相反的利益,一方最大化这个利益,另外一方最小化这个利益:
两人对决游戏 (MAX and MIN, MAX 先走) 可如下形式化描述:
| 形式化描述 | |
|---|---|
| 状态 | 状态 s 包括当前的游戏局面和当前行动的智能体 函数 player (s) 给出状态 s 下行动的智能体 |
| 动作 | 给定状态 s,动作指的是 player (s) 在当前局面下可以采取的操作 a 记动作集合为 actions (s) |
| 状态转移 | 给定状态 s 和动作 a∈actions (s),状态转移函数 result (s, a) 决定了在 s 状态采取 a 动作后所得后继状态 |
| 终局状态检测 | 终止状态检测函数 terminal_test (s) 用于测试游戏是否在状态 s 结束。 |
| 终局得分 | 终局得分 utility (s, p) 表示在终局状态 s 时玩家 p 的得分。 |
本次讨论中,主要讨论在**确定的、全局可观察的、竞争对手轮流行动、零和游戏(zero-sum)**下的对抗搜索
最小最大搜索 (Minimax Search)
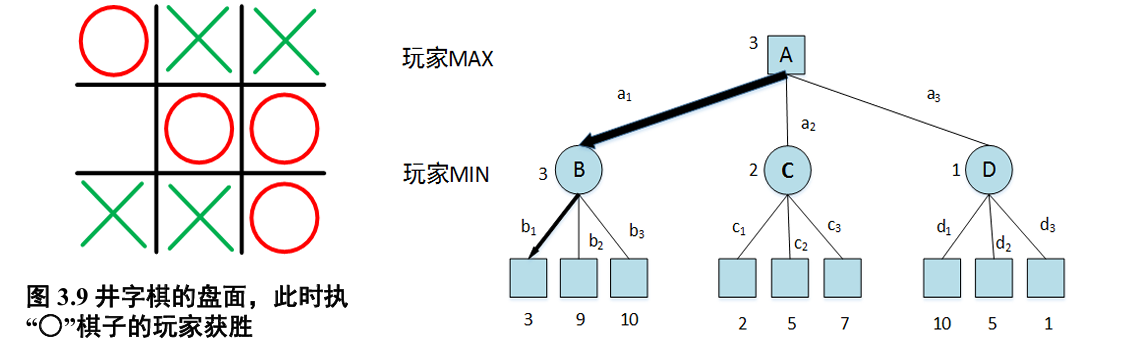
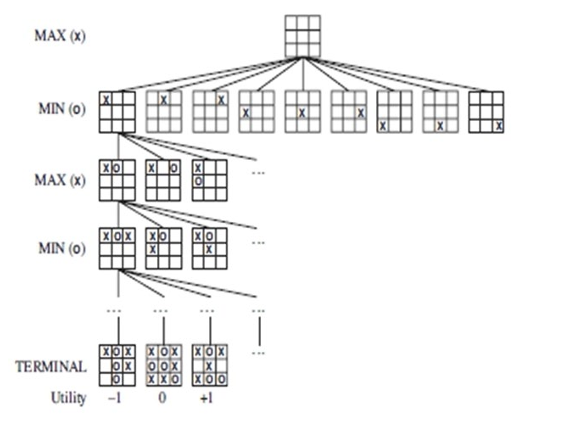
给定一个游戏搜索树,minimax 算法通过每个节点的 minimax 值来决定最优策略
- MAX 希望最大化 minimax 值,
- MIN 则相反
性能分析
- 完备性: Yes (if the tree is finite)
- 最优性: Yes (against an optimal opponent)
- 时间复杂度:
- Depth-first exploration
执行了一个完整的深度优先搜索
- Depth-first exploration
- 空间复杂度:
- Depth-first exploration
Alpha-Beta 剪枝搜索 (Pruning Search)
Alpha-Beta 剪枝搜索算法在 Minimax 算法中可减少被搜索的结点数,即在保证得到与原 Minimax 算法同样的搜索结果时,剪去了不影响最终结果的搜索分枝
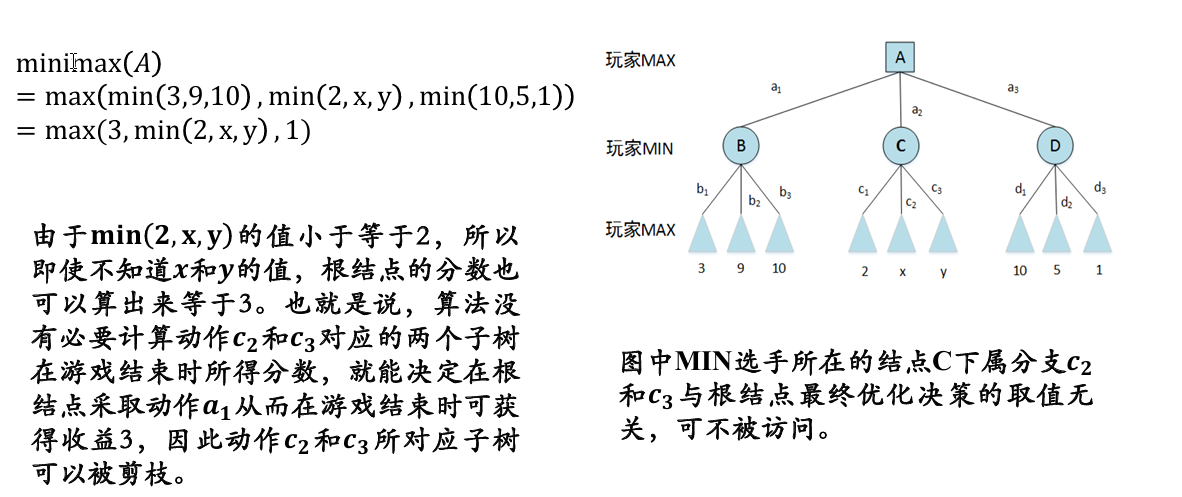
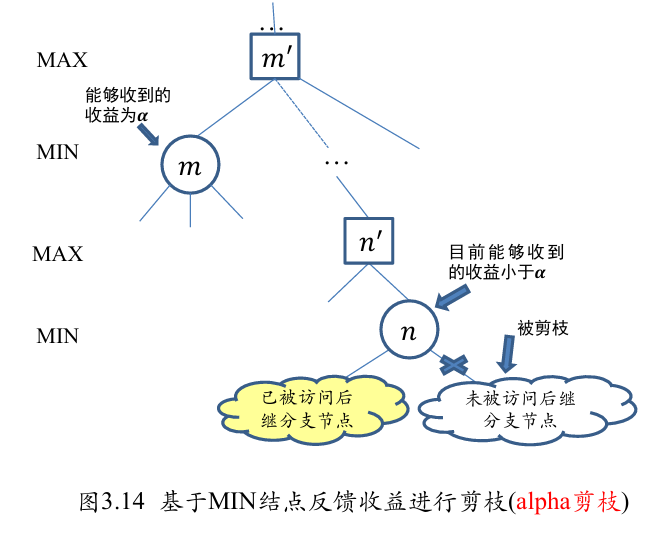
Alpha 剪枝
- 假设有一个位于 MIN 层的结点
, 已知该结点能够向其上 MAX 结点反馈的收益为 是与结点 位于同一层的某个兄弟 (sibling) 结点的后代结点 - 如果在结点
的后代结点被访问一部分后,知道结点 能够向其上一层 MAX 结点反馈收益小于 , 则结点 的未被访问孩子结点将被剪枝
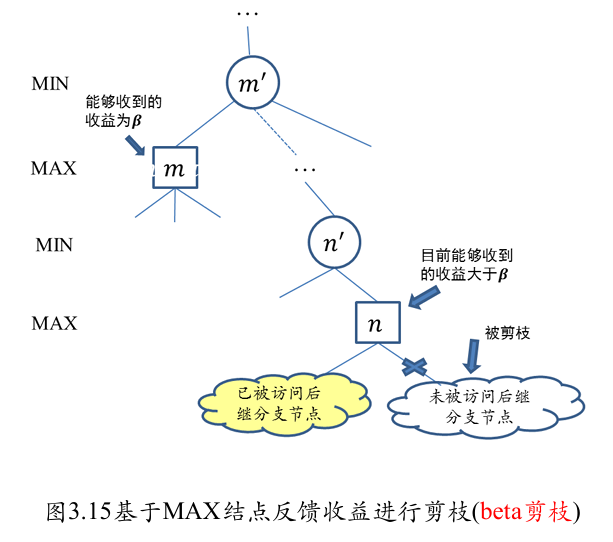
Beta 剪枝
- 考虑位于 MAX 层的结点
, 已知结果点 能够从其下 MIN 层结点收到的收益为 - 结点
是结点 上层结点 的位于 MAX 层的后代结果点 - 如果目前已知结点
能够收到的收益大于 , 则不再扩展结点 的未被访问后继结点,因为位于 MIN 层的结点 只会选择收益小于或等于 的结点来采取行动
算法流程
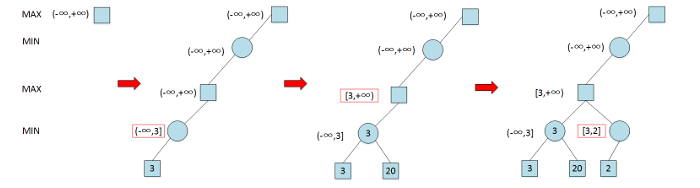
- 根结点(MAX 结点)的𝛼值和𝛽值分别被初始化为−∞和+∞
- 子节点继承父节点的𝛼值和𝛽值,再按照以下规则进行更新
- 对于 MAX 节点,如果其孩子结点(MIN 结点)的收益大于当前的𝛼值(极大层的下界),则将𝛼值更新为该收益
- 对于 MIN 结点,如果其孩子结点(MAX 结点)的收益小于当前的𝛽值(极小层的上界),则将𝛽值更新为该收益
- 如果一个结点的𝛼值和𝛽值满足𝛼>𝛽的条件,则该结点尚未被访问的后续结点就可以被剪枝
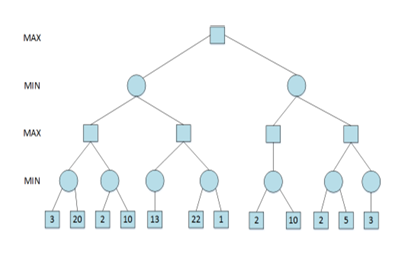
原本 Minimax 搜索树中有 26 个结点,经过 alpha-beta 剪枝后只扩展(访问)了其中 15 个结点,可见 alpha-beta 剪枝技术能够有效地减少搜索树中结点的数目
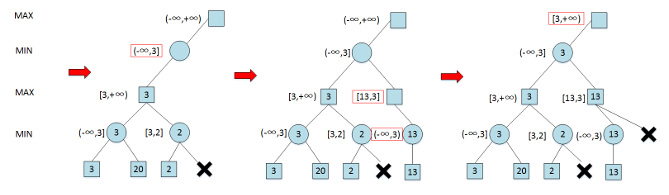
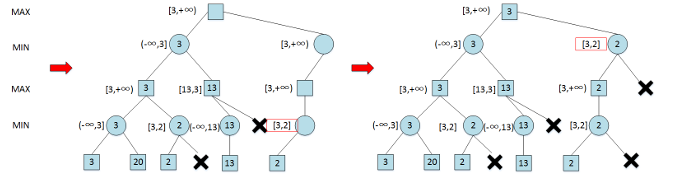
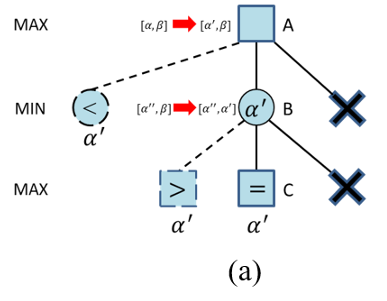
使用反证法即可
2.4 蒙特卡洛搜索
引入:多臂赌博机问题
问题描述:
- 假设智能体面前有𝑲个赌博机,每个赌博机有一个臂膀
- 每次转动一个赌博机臂膀,随机吐出一些硬币或不吐出硬币,将所吐出的硬币的币值用收益分数来表示
- 现在假设给智能体 𝝉 (𝛕 > 𝐊) 次转动臂膀的机会
- 智能体如何选择赌博机、转动 𝝉 次赌博机臂膀,能够获得更多的收益分数
形式化分析
- 状态:每个被摇动的臂膀即为一个状态,记
个状态分别为 , 没有摇动任何臂膀的初始状态记为 - 动作: 动作对应着摇动一个赌博机的臂膀,在多臂赌博机问题中,任意状态下的动作集合都为
..., - 状态转移:选择动作
后,将相应的改变为 - 奖励 (reward)
- 假设从第
个赌博机获得收益分数的分布为 , 其均值为 - 如果智能体在第
次行动中选择转动了第 个赌博机臂膀,那么智能体在第 次行动中所得收益分数 服从分布 被称为第 次行动的奖励 - 一般假定奖励是有界的,进一步可假设奖励的取值范围为[0,1]
- 假设从第
- 悔值 (regret) 函数。根据智能体前
次动作,可以如下定义悔值函数: 其中 。
因此,问题求解的目标为最小化悔值函数的期望,该悔值函数的取值取决于智能体所采取的策略
智能体不能预先计算好最优策略,然后实行,而是需要一边探索一边调整自己的策略,争取获得更好的收益
贪心算法策略
贪心算法策略如下:
- 给定第
个赌博机,记在过去 次摇动赌博机臂膀的行动中,一共摇动第 个赌博机臂膀的次数为第 - 第
个赌博机在过去 次被摇动过程中的收益分数平均值 - 在第
步,只要选择 值最大的赌博机臂膀进行摇动
不足:忽略了其他从未摇动或很少摇动的赌博机,而失去了可能的机会 👇 探索与利用结合
𝝐-贪心算法
不足:与被探索的次数无关 👉 需要对那些探索次数少或几乎没有被探索过的动作赋予更高的优先级
上限置信区间算法(Upper Confidence Bounds, UCB 1)
在第
优先采用探索估计值不确定度高的动作
算法流程
如何高效地拓展搜索树:
- 优先拓展哪些节点
- 放弃拓展哪些节点
目标降低,改为求解一个近似最优解:
- 每一步动作为选择(在非叶子节点) 或拓展(在叶子节点) 一个孩子节点
- 通过采样式探索来得到计算奖励的样本
- 选择 (selection)
- 算法从搜索树的根节点开始,向下递归选择子节点,直至到达叶子节点或者到达具有还未被扩展过的子节点的节点 L
- 这个向下递归选择过程可由 UCB 1 算法来实现,在递归选择过程中记录下每个节点被选择次数和每个节点得到的奖励均值
- 扩展 (expansion)
- 如果节点 L 不是一个终止节点 (或对抗搜索的终局节点), 则随机扩展它的一个未被扩展过的后继边缘节点 M
- 模拟 (simulation)
- 从节点 M 出发,模拟扩展搜索树,直到找到一个终止节点
- 模拟过程使用的策略和采用 UCB 1 算法实现的选择过程并不相同
- 模拟过程通常会使用比较简单的策略,例如使用随机策略
- 反向传播 (Back Propagation)
- 用模拟所得结果 (终止节点的代价或游戏终局分数) 回溯更新模拟路径中 M 以上 (含 M) 节点的奖励均值和被访问次数
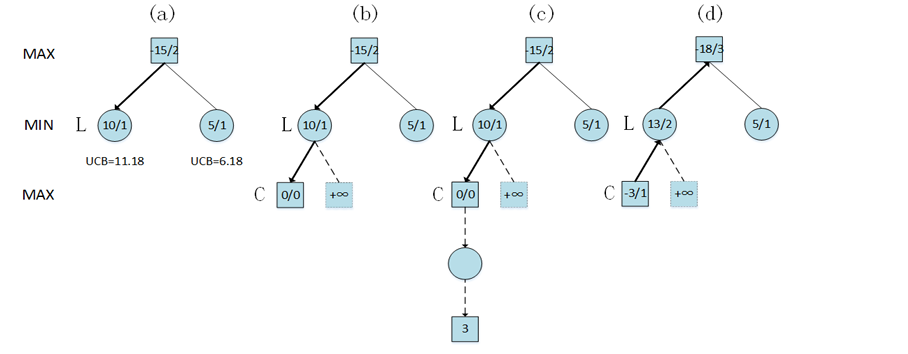
选择阶段
- 计算第二层节点的 UCB 值:左侧结点为
, 右侧结点为 - 因此算法选择第二层左侧的结点 L,由于该节点有尚未扩展的子结点,因此选择阶段结束
拓展阶段
- 在图 3.25 (b) 中,算法随机扩展了 L 的子结点 C,将其总分数和被访问次数均初始化为 0
- 图 3.25 (b) 画出了 L 的其他未被扩展的子结点,并标记其 UCB 值为正无穷
- 表示算法下次访问到 L 时必然扩展这些未被扩展的结点
模拟阶段
- 采用随机策略模拟游戏直至完成游戏。当游戏完成时,终局得分为 3
反向传播阶段
- 更新策略为:MIN 层结点现有总分加上终局得分分数,MAX 层结点现有总分减去终局得分分数
- 在图 (d) 中
- C 结点的总分被更新为-3,被访问次数被更新为 1
- L 结点的总分被更新为 13,被访问次数被更新为 2
- 根结点的总分被更新为-18,被访问次数被更新为 3
03 机器学习
- 从数据利用的角度,ML 划分为监督学习、无监督学习及半监督学习
- 有监督学习:训练集、验证集、测试集
- 模型评估与参数估计手段:损失函数
- 经验风险与期望风险
- 经验风险最小化与过学习 (overfitting)
- 模型的泛化能力:在机器学习中,需要保证模型在训练集上所取得性能与在测试集上所取得性能保持一致
- 模型泛化能力与经验风险和期望风险之间关系
- 结构风险最小化 (structural risk minimization) 引入正则化 (regularizer) 或惩罚项 (penalty term) 来降低模型模型复杂度,既最小化经验风险、又力求降低模型复杂度,在两者之间寻找平衡:
- 模型度量方法:准确率、错误率、精确率、召回率、综合分类率 F1-score(
) - 监督学习:
- 回归分析(线性 vs 非线性)
- 决策树(信息熵、信息增益
、信息增益率、Gini 系数) - 线性判别分析(LDA,基于监督学习的降维方法,最大化的目标
, )
- 无监督学习:
- K 均值聚类:通过最小化聚簇内的数据方差来实现最大化类内相似度的
- 主成分分析:无监督特征降维方法,要求最大限度保持原始高维数据的总体方差结构。应用于基于特征人脸的识别
- 演化算法:遗传算法 (genetic algorithm)、遗传规划 (genetic programming, GP)、演化策略 (evolutionary strategy)
3.1 机器学习基本概念
通过对数据的优化学习,建立能够刻画数据中所蕴含语义概念或分布结构等信息的模型
数据利用的角度分类:
- 监督学习
- 无监督学习
- 半监督学习
监督学习
监督学习:带有标签信息数据的训练集
- 从假设空间学习得到一个最优映射函数 f (决策函数)
数据集可分为:
- 训练集:模型训练 👉 学生的练习册
- 验证集:评估模型,调整参数 👉 模拟考
- 测试集:得到模型的优劣水平 👉 真正考试
任何一个机器学习模型如果在一些训练集以外的样本上误差小(off-training set error),那么必然在另外一些训练集以外的样本上表现欠佳,任何模型在平均意义上而言其性能都是一样的,即没有放之四海而皆准的最好算法
实践经验:在机器学习中合理引入已有先验假设对模型进行约束,以提升模型效果
泛化能力
- 模型在训练集上的性能和测试集一致
在训练过程中,映射函数 f(学习模型)的主要目标是最小化整个训练数据集上的累积“损失”。 这可以表示为:
经验风险 empirical risk 与期望风险 expected risk
- 经验风险是训练集中数据产生的损失
- 期望风险是当测试集中存在无穷多数据时产生的损失
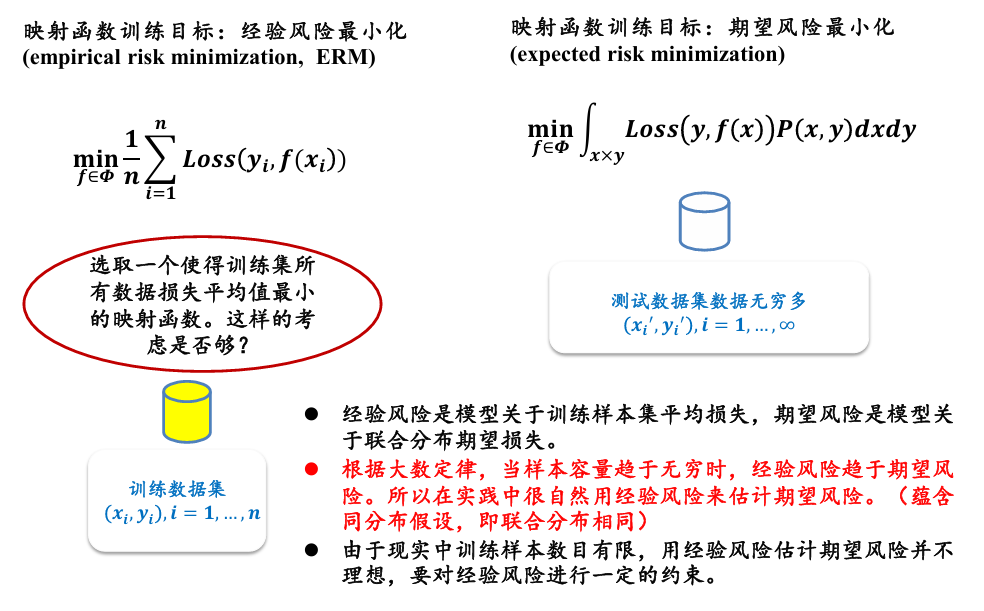
期望风险(即真实风险)
- err 与训练样本个数和模型复杂度都有密切的关系
“过学习 (over-fitting)”与“欠学习 (under-fitting)”
- Over-fitting:经验风险小而期望风险大
- Under-fitting:经验风险大且期望风险大
结构风险最小化 structural risk minimization
- 经验风险最小化:仅反映了局部数据
- 期望风险最小化:无法得到全量数据
- 为了防止过拟合,在经验风险上加上表示模型复杂度的正则化项 (regulatizer) 或惩罚项 (penalty term )
在最小化经验风险与降低模型复杂度之间寻找平衡
模型度量方法
以二分类问题为例:n 为训练样例总数,正例为 P,负例为 N;
TP 真正例 👉 模型预测为正,实际为正
FP 假正例 👉 模型预测为正,实际为负
TN 真负例 👉 模型预测为负,实际为负
FN 假负例 👉 模型预测为负,实际为正
- 准确性 (accuracy):
- 很显然,如果正负样本比例不平衡,ACC 不是一个度量模型好的方法。比如,某一种恶性疾病很罕见(如 1 万个疑似患者中仅有 1 人罹患该疾病),机器学习模型可将所有患者均识别为负类,从而保证 ACC 取值极高,但这就忽略了这一模型应该关注的问题。
- 错误率 (error rate):
- 显然有
- 显然有
- 精确率 (precision):
- 也叫查准率,表示被模型预测为正例的样本中实际为正例的比例
- 召回率 (Recall):
- 也叫查全率,表示所有正例样本中被模型预测为正例的比例
在实际应用中,精确率和召回率之间是相互矛盾的,比如可以将所有样本分类为正例使得召回率为 100%而精确率极低。因此为了综合考虑精确率和召回率,可采用综合分类率 F1-score:
F1-score 是精确率和召回率的调和平均数,在尽可能提高精确率和召回率同时,也希望两者之间的差异尽可能小
3.2 回归分析
分析不同变量之间存在关系的研究叫回归分析,刻画不同变量之间关系的模型被称为回归模型
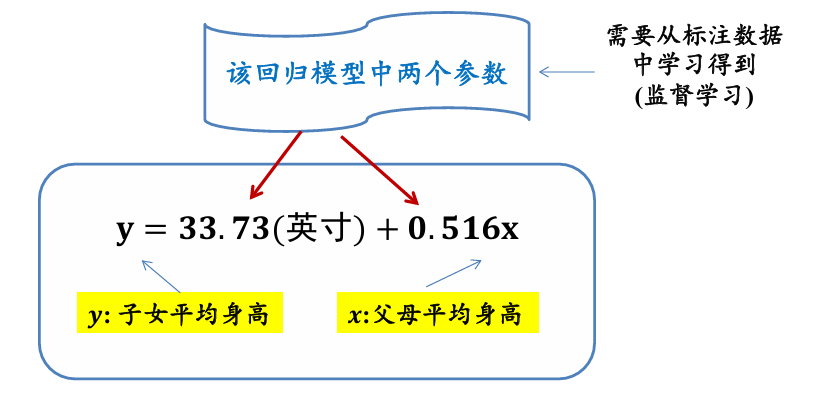
一元线性回归
回归模型参数求取:
- 记在当前参数下第
个训练样本 的预测值为 的标注值(实际值) 与预测值 之差记为 - 训练集中
个样本所产生误差总和为:
目标: 寻找一组
- 一般而言,要使函数具有最小值,可对
参数 和 分别求导,令其导数值为零,再求取参数 和 的取值
多元线性回归
多维数据特征中线性回归的问题定义如下:假设总共有
最小化均方误差函数:
为了方便,使用矩阵来表示所有的训练数据和数据标签。
其中每一个数据
均方误差函数可以表示为:
均方误差函数
因为均方误差函数
逻辑斯蒂回归/对数几率回归
线性回归一个明显的问题是对离群点非常敏感,导致模型建模不稳定,使结果有偏
逻辑斯蒂回归 (logistic regression) 就是在回归模型中引入 sigmoid 函数的一种非线性回归模型。Logistic 回归模型可如下表示:
这里
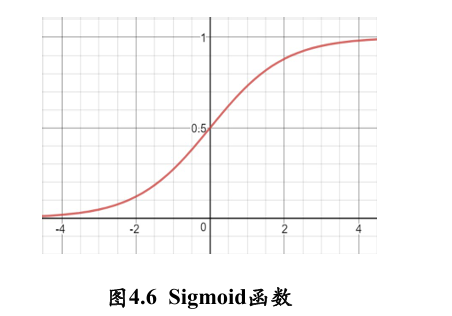
logistic 回归只能用于解决二分类问题,将它推广为多项逻辑斯蒂回归模型 (multi-nominal
logistic model, 即 softmax 函数), 用于处理多类分类问题,可以得到处理多类分类问题的 softmax 回归
3.3 决策树
- 非叶子节点:对分类目标某一属性的判断
- 叶子节点:分类结果
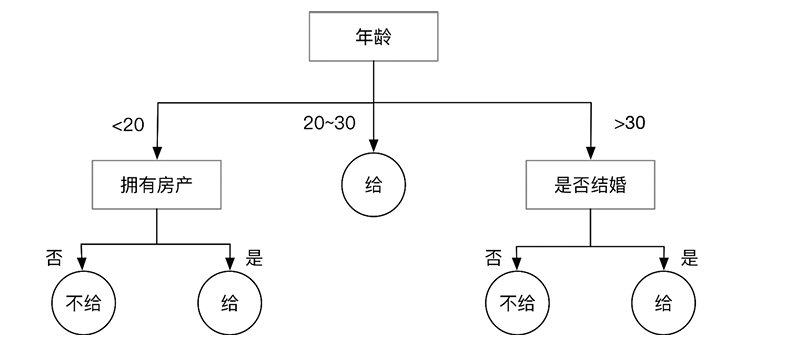
建立决策树的过程,就是不断选择属性值对样本集进行划分,直至每个子样本为同一个类别
构建决策树时划分属性的顺序选择是重要的。性能好的决策树随着划分不断进行,决策树分支结点样本集的“纯度”会越来越高,即其所包含样本尽可能属于相同类别
信息增益
信息熵(entropy)是度量样本集合纯度最常用的一种指标:如果我们计算选择不同属性划分后样本集的“纯度”, 那么就可以比较和选择属性。信息熵越大,说明该集合的不确定性越大,“纯度”越低
假设有
值越小,表示 包含的信息越确定,也称 的纯度越高 - 所有
累加起来的和为 1 - 约定:若
, 则
选择属性划分样本集前后信息熵的减少量被称为信息增益 (information gain), 也就是说信息增益被用来衡量样本集合复杂度 (不确定性) 所减少的程度
信息增益的计算:
- 通过比较样本的属性信息增益的高低来选择最佳属性(信息增益最大的属性)对原样本集进行划分,得到最大的“纯度”
- 如果划分后的不同子样本集都只存在同类样本 (类别标签一致),那么停止划分
"给予贷款"是本次数据的标签,初始 D 的信息熵的计算直接基于此:




信息增益率和基尼系数
信息增益率:新的指标 👉 对分支过多进行惩罚
Info 和 Gain-ratio(增益率)计算公式如下:
一个启发式:
- 先从候选划分属性中找出信息增益高于平均水平的属性
- 再从中选取增益率最高的
更简的度量指标是如下的 Gini 指数(基尼指数):
- 相对于信息熵的计算
,不用计算对数 log,计算更为简易
3.4 K-means
- 若干定义:
- n 个 m-维数据
, (1≤i≤n) - 两个 m 维数据之间的欧氏距离为
值越小,表示 和 越相似;反之越不相似
- n 个 m-维数据
- 聚类集合数目 k
- 问题: 如何将 n 个数据依据其相似度大小将它们分别聚类到 k 个集合,使得每个数据仅属于一个聚类集合
- 初始化聚类质心
- 初始化
个聚类质心 - 每个聚类质心
所在集合记为
- 初始化
- 将每个待聚类的数据放入唯一一个聚类集合中
- 计算待聚类数据
和质心 之间的欧氏距离 - 将每个
放入与之距离最近聚类质心所在聚类集合中,即
- 计算待聚类数据
- 更新聚类质心
- 根据每个聚类集合中所包含的数据,更新该聚类集合质心值,即:
- 根据每个聚类集合中所包含的数据,更新该聚类集合质心值,即:
- 算法迭代,直至满足条件
- 迭代次数上限
- 质心基本不变
聚类算法的目标都是得到一个聚类结果,最小化类内距离(或最大化类内相似度),而最大化类间距离(或最小化类间相似度)
使得最终聚类结果中每个聚类集合所包含的数据呈现出的差异性最小
3.5 监督学习与非监督学习下的特征降维
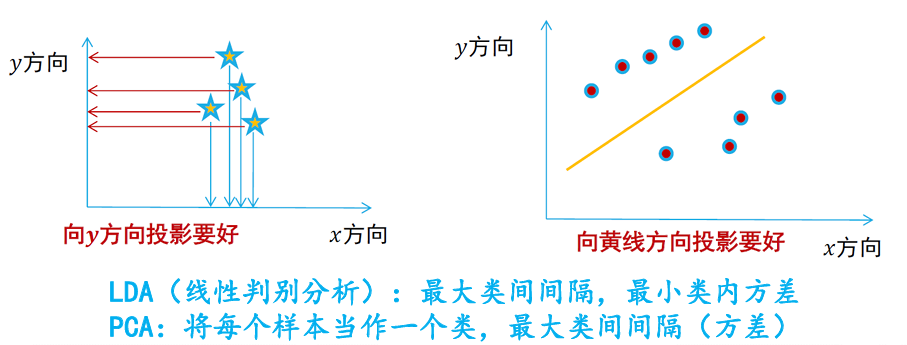
线性判别分析 LDA
线性判别分析 (linear discriminant analysis, LDA)
也称为 Fisher 线性判别分析(fisher'sdiscriminant analysis,FDA) [Fisher 1936]
在低维空间中同一类别样本尽可能靠近,不同类别样本尽可能彼此远离
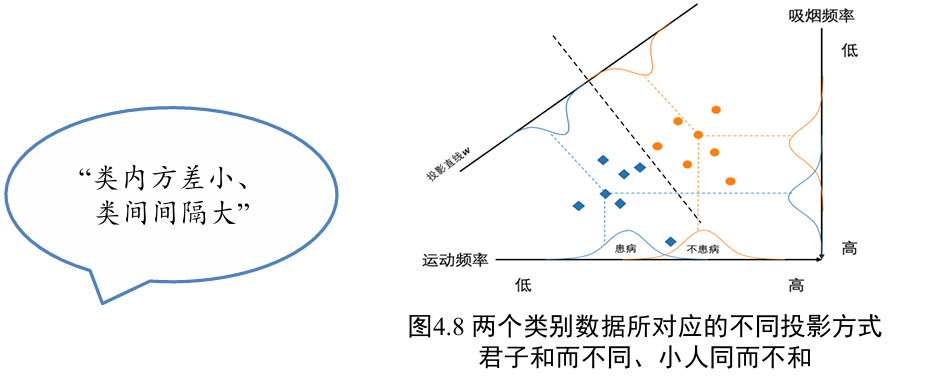
符号定义:
- 样本集为
- 样本
的类别标签为 的取值范围是 ,即一共有 K 类样本
定义 X 为所有样本构成集合、
- 协方差矩阵,衡量的是原始
各个维度 之间的关联性
我们考虑二分类问题,即 K = 2 的情况
在二分类问题中,训练样本归属于
- 通过一个 d 维的参数,将原始数据 x 降到一维空间
投影之后类别
- 为了使得归属于同一类别的样本数据在投影后的空间中尽可能靠近,需要最小化 s1+s2 取值(类内方差小)
- 为了使得归属于不同类别的样本数据在投影后空间中尽可能彼此远离,需要最大化过
取值 (类间间隔大)
同时考虑上面两点,就得到了需要最大化的目标
称为类间散度矩阵 (between-class scatter matrix),衡量两个类别均值点之间的“分离”程度,可定义如下:
则称为类内散度矩阵 (within-class scatter matrix),衡量每个类别中数据点的“分离”程度,可定义如下:
由于
对应拉格朗日函数为:
对
因为
由于对
为了获得“类内汇聚、类间间隔”的最佳投影结果,只需要分别求出待投影数据的均值和方差,就可以设计得到最佳投影方向
将原始数据通过
令投影矩阵
- 给定原始
维空间中的数据样本 , 通过 将其从 维空间映射到 维空间 - 在后续分类等操作中,只是使用
降维后的结果,而不是 的原始特征
- 计算数据样本集中每个类别样本的均值
- 计算类内散度矩阵
和类间散度矩阵 - 根据
来求解 所对应前 个最大特征值所对应特征向量 ,构成矩阵 - 通过矩阵
将每个样本映射到低维空间,实现特征降维
通过 LDA 对原始 d 维数据进行降维后,所得维度 r 最大取值为
- 因为
的秩为 - 说明二分类问题中,原始高维数据只能被投影到一维空间中
主成分分析 PCA
也叫 KL 变换,霍林特变换、本征正交分解
最大限度保持原始高维数据的总体方差结构
- 协方差
- 对象:n 个 2 维变量数据
- 衡量两个变量之间的相关度
- 对象:n 个 2 维变量数据
- Pearson Correlation coefficient
- 将两组变量的关联度规整到一定的范围内
- 性质:
的充要条件是存在常数 和 , 使得 - 皮尔逊相关系数是对称的,即 corr
- 作用:刻画两个变量之间的线性相关度
- 如果
的取值越大,则两者在线性相关的意义下相关程度越大 表示两者不存在线性相关关系 (可能存在其他非线性相关的关系)
- 如果
- 将两组变量的关联度规整到一定的范围内
- 相关性 correlation 与独立性 independence
- 如果 X 和 Y 的线性不相关,则
- 如果
和 的彼此独立,则一定 , 且 和 Y 不存在任何线性或非线性关系 - “线性无关” 比 “独立” 弱
- 如果 X 和 Y 的线性不相关,则
主成分分析:特征降维的方法,但要保证降维后的结果要保持原始数据固有结构
- 需要尽可能将数据向方差最大方向进行投影,使得数据所蕴含信息没有丢失,彰显个性
- 将𝒅维特征数据映射到𝒍维空间(𝒅≫𝒍),去除原始数据之间的冗余性(通过去除相关性手段达到这一目的)
- 将原始数据向这些数据方差最大的方向进行投影。一旦发现了方差最大的投影方向,则继续寻找保持方差第二的方向且进行投影(保证方向的正交性)
| 线性判别分析 | 主成分分析 | |
|---|---|---|
| 是否需要样本标签 | 监督学习 | 无监督学习 |
| 降维方法 | 优化寻找特征向量 |
优化寻找特征向量 |
| 目标 | 类内方差小、类间距离大 (这里的类就是由数据带有的标签决定的) |
寻找投影后数据之间方差最大的投影方向 |
| 维度 | LDA 降维后所得到维度是与数据样本的类别个数 |
PCA 对高维数据降维后的维数是与原始数据特征维度相关 |
- 输入:n 个 d 维样本数据所构成的矩阵 X,降维后的维数为 l
- 输出:映射矩阵
- 对于每个样本数据
进行中心化处理: - 计算原始样本数据的协方差矩阵:
- 对协方差矩阵
进行特征值分解,对所得特征根按其值大到小排序 - 取前
个最大特征根所对应特征向量 组成映射矩阵 W - 将每个样本数据
按照如下方法降维:
特征人脸
使用一组特征向量的线性组合来表示原始人脸
- 用(特征)人脸表示人脸,而非用像素点表示人脸
- 将每幅人脸图像转换成列向量
- 如将一幅 32 × 32 的人脸图像转成 1024 × 1 的列向量
- 每幅人脸分别与每个特征人脸做矩阵乘法,得到相关系数
- l 个相关系数
- 输入:
个 1024 维人脸样本数据所构成的矩阵 X,降维后的维数 - 输出:映射矩阵 W
其中每个 j 是一个特征人脸)
算法步骤:
- 对于每个人脸样本数据
进行中心化处理: - 计算原始人脸样本数据的协方差矩阵:
用代替大的协方差矩阵计算,避免 d 维度过高计算复杂 - 对协方差矩阵
进行特征值分解,对所得特征根从到小排序 - 取前
个最大特征根所对应特征向量 组成映射矩阵 W - 将每个人脸图像
按照如下方法降维:
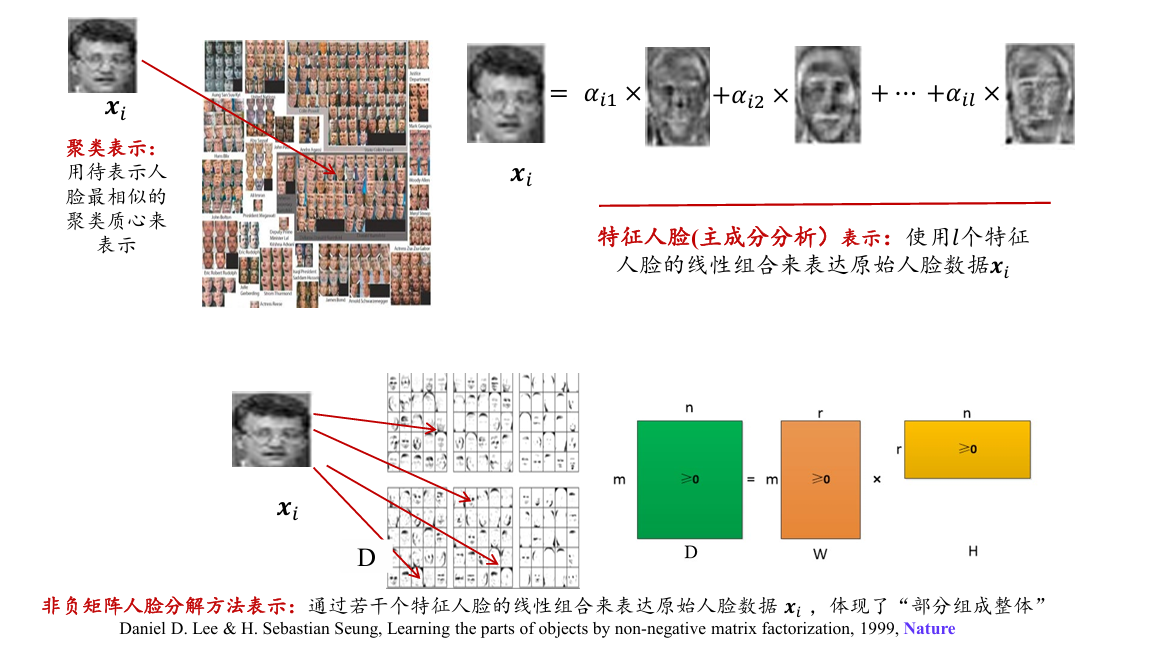
在特征维度较高的情况下,主成分分析算法暴力求解特征向量是一个耗时操作。可以使用一种矩阵分解方法——奇异值分解(singular value decomposition, SVD)来实现主成分分析,对原始数据进行降维
- 用
代替大的协方差矩阵计算,避免 d 维度过高计算复杂
3.6 演化算法
演化算法:一大类受自然演化启发的启发式随机优化算法,通过“突变重组”和“自然选择” 这两种机制来模拟自然演化过程
- 遗传算法 (genetic algorithm)
- 遗传规划 (genetic programming,GP)
- 演化策略 (evolutionary strategy)
- ...
遗传算法:引入选择 (selection)、交叉 (crossover) 和变异 (mutation) 等操作以搜索方式来进行优化求解
- 对于一个待求解的最优化问题,先给定一定数量候选解 👉 个体/染色体
- 然后让这些染色体所构成种群,向最优解进化
- 在每一次进化过程中,计算每个染色体(即候选解)的适应度(fitness),根据适应度选择合适染色体
- 随后施以选择和变异来产生新的生命种群,该种群在算法下一次迭代中被作为当前种群
- 初始化:初始化具有若干规模数目的群体。当前进化代数 Generation=0
- 计算适应值:采用评估函数计算群体中每个染色体的适应值,保存适应值最大的染色体 Best
- 选择:采用轮盘赌选择算法对群体中染色体进行选择,产生同样规模的种群
- 轮盘赌选择算法 👉 适应值越大,选中的概率就越大
- 交叉:按照概率从种群中选择两对染色体进行交叉操作,即对所选中两对染色体中相应基因片段信息进行交换
- 交叉所得染色体进入新种群,未交叉操作染色体被复制进入新种群
- 变异:按照概率对新种群中被选中染色体的若干基因片段进行变异操作
- 变异后染色体取代原有染色体进入新种群,未发生变异染色体直接进入新群体
- 更新 Best:计算种群中各个染色体的适应值。倘若种群中染色体最大适应值大于已知 Best 适应值,则取代原有 Best
- 当前进化代数 Generation 加 1。如果 Generation 超过规定的最大进化代数或 Best 达到规定的误差要求,算法结束:否则返回步骤 3






04 神经网络与深度学习
- MCP 模型、单层感知机、多层感知机(也叫前馈神经网络,由输入层、输出层和若干隐藏层构成)
- 激活函数(非线性映射):sigmoid、ReLU、Tanh、Leaky ReLU、Parametric ReLU、Softmax
- 损失函数:均方误差损失函数(
)、交叉熵损失函数( ) - 误差反向传播算法:将损失函数计算所得误差从输出端出发、由后向前传递给神经网络中每个单元
- 梯度下降算法:对神经网络中参数进行更新,使损失函数最小化的方法
- 批量梯度下降算法、随机梯度下降算法和小批量梯度下降算法
- 梯度消失和梯度爆炸
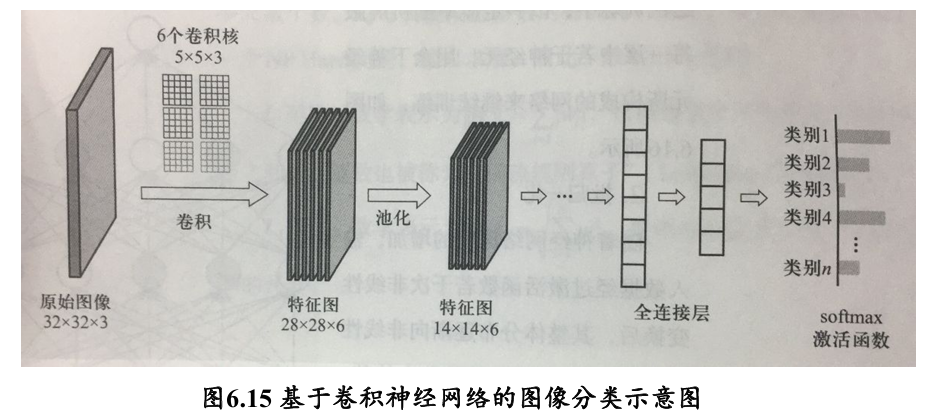
- 卷积神经网络:
- 卷积操作:特征图、填充 (padding)、步长 (striding)
- 池化操作:最大池化(max pooling)、平均池化(average pooling)、k-max 池化(k-max pooling)
- 特点:选择性感受野、局部感知、参数共享、采样约减抽象
- 循环神经网络:RNN、长短时记忆模型 LSTM(内部记忆单元、三种门结构、减弱梯度消失)
- 注意力机制:自注意力(self-attention)、多头注意力(multi-headed attention)
- 神经网络正则化:Dropout、批归一化(batch normalization)、L1 和 L2 正则化
- 词向量生成:Word2Vec 模型
4.1 前馈神经网络与参数优化
神经网络基本单元:MCP 神经元
神经元因何连接:赫布理论
神经元链接成"网":感知机
基本概念
神经元是深度学习模型中基本单位。可以如下刻画神经元功能:
- 对相邻前向神经元输入信息进行加权累加:
- 对累加结果进行非线性变换 (通过激活函数)
- 神经元的输出:Out
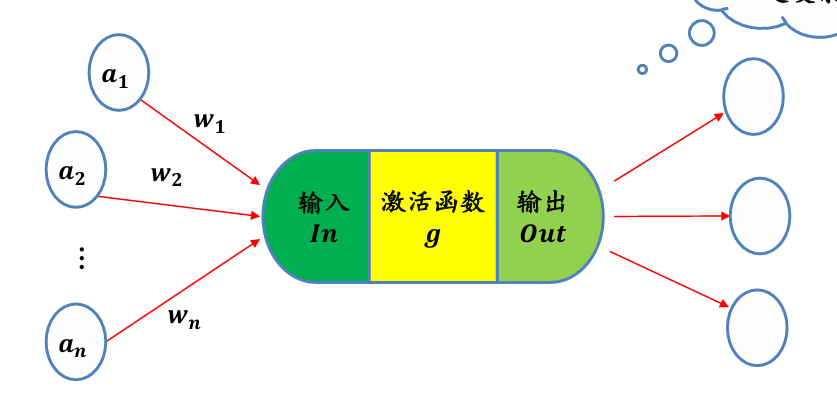
神经网络使用非线性函数作为激活函数(activation function),通过对多个非线性函数进行组合,来实现对输入信息的非线性变换:
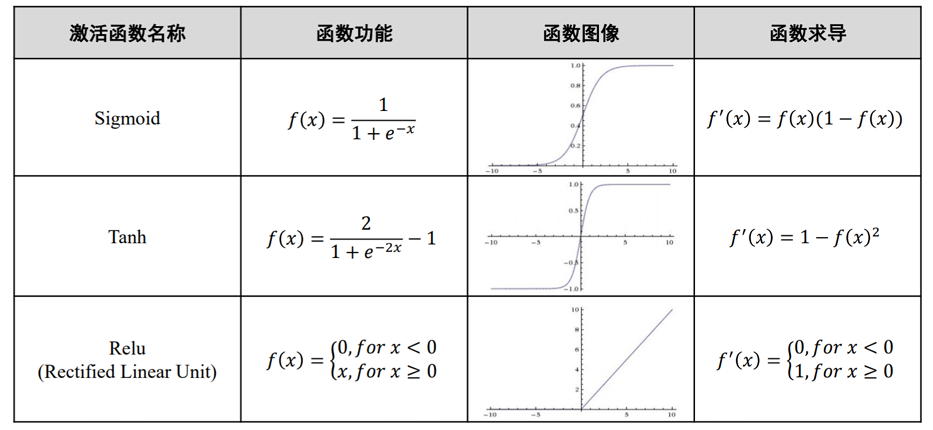
- 概率形式输出:函数是单调递增的,其值域为 (0,1), 可用作概率值
- 单调递增:对输入 z 没有取值范围限制,但当 z 大于 (小于) 一定数值后,函数输出无限逼近 1 (0), 当 z 等于 0 时,函数输出为 0.5
- 非线性变化:z 取值在 0 附近时,函数输出值变化比较大,且是非线性变化,但 z 取值很大或很小时,函数输出值几乎不变
sigmoid 函数导数小于 1,在使用反向传播更新参数,容易出现导数过于接近 0 的情况
- 当输入
时,ReLU 的导数为常数,这样可有效缓解梯度消失这一问题 - 当输入
时,ReLU 的梯度总是 0,导致神经网络中若干参数激活值为 0,即参与分类等任务神经元数目稀缺,这种稀疏性可以在一定程度上克服机器学习中经常出现的过拟合现象 - 然而,当 x<0 时,ReLU 梯度为 0 也导致神经元“死亡”, 即神经元对应权重永远不会更新
- 为了解决这个问题,可以使用其他激活函数,如 Leaky ReLU 或 Parametric ReLU, 它们在 x<0 时梯度取值非零
Softmax 函数一般用于多分类问题中,其将输入数据
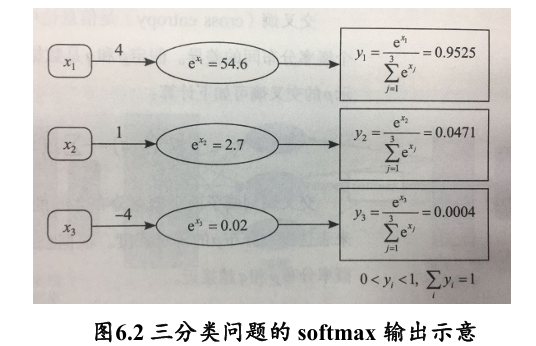
感知机模型
早期的感知机结构和 MCP 模型相似,由一个输入层和一个输出层构成,因此也被称为 “单层感知机”。感知机的输入层负责接收实数值的输入向量,输出层则能输出 1 或 -1 两个值
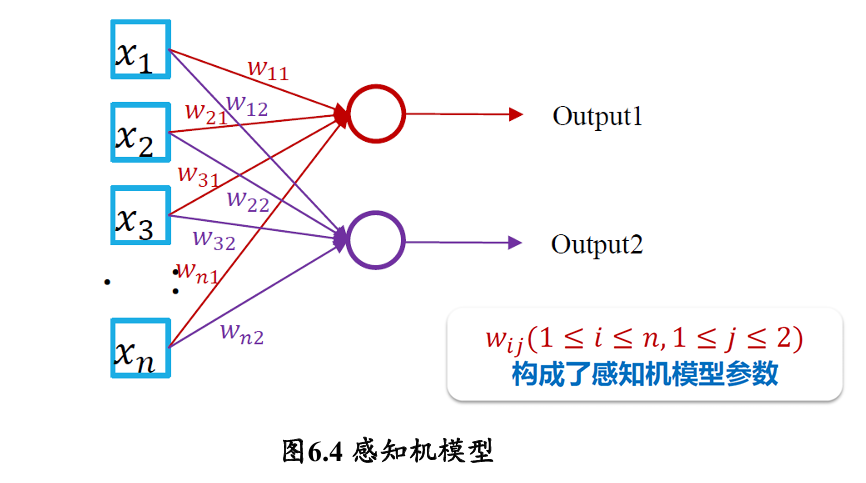
单层感知机可以作为一种线性二分类模型
单层感知机可模拟逻辑与 (AND)、逻辑与非 (NAND) 和逻辑或 (OR) 等线性可分函数,但是无法完成逻辑异或 (XOR) 这一非线性可分逻辑函数任务
多层感知机由输入层、输出层和至少一层的隐藏层构成 👉也叫做前馈神经网络
- 网络中各个隐藏层中神经元可接收相邻前序隐藏层中所有神经元传递而来的信息,经过加工处理后将信息输出给相邻后续隐藏层中所有神经元。
- 各个神经元接受前一级的输入,并输出到下一级,模型中没有反馈
- 层与层之间通过“全连接”进行链接,即两个相邻层之间的神经元完全成对连接,但层内的神经元不相互连接
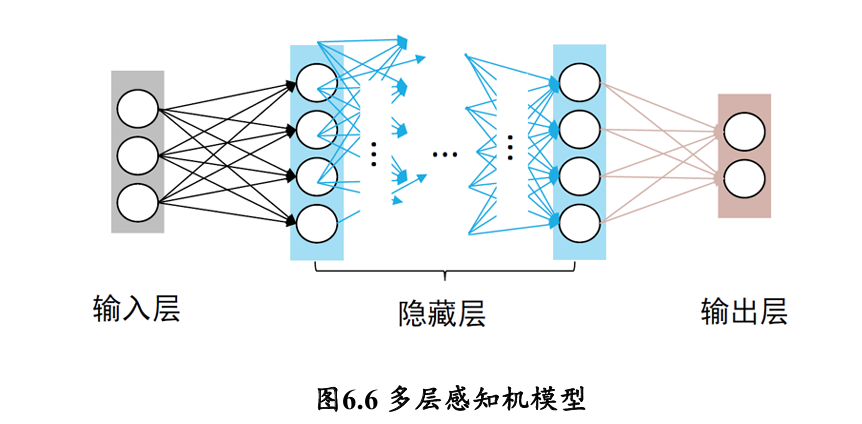
如何优化网络参数?
从标注数据出发,优化模型参数:监督学习过程
- 标注数据:
- 评分函数 (scoring function) 将输入数据映射为类别置信度大|小:s
- 损失函数来估量模型预测值与真实值之间的差距。损失函数给出的差距越小,则模型鲁棒性就越好。
- 常用的损失函数有 softmax 或者 SVM
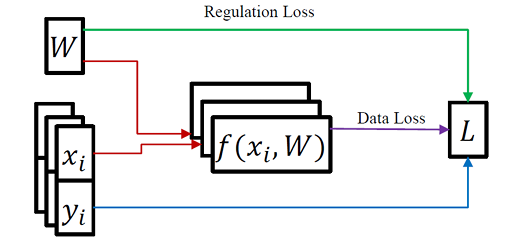
- 常用的损失函数有 softmax 或者 SVM
损失函数(Loss Function):计算模型预测值与真实值之间的误差
- 均方误差损失函数:计算预测值和实际值之间距离(即误差)的平方来衡量模型优劣
- 交叉熵损失函数:度量两个概率分布间的差异
是样本 分类的真实概率分布、 是模型预测概率分布
交叉熵越小,两个概率分布和 越接近
梯度下降 Gradient Descent
梯度下降算法是一种使得损失函数最小化的方法。一元变量所构成函数𝒇在𝒙处梯度为:
- 在多元函数中,梯度是对每一变量所求导数组成的向量
- 梯度的反方向是函数值下降最快的方向,因此是损失函数求解的方向
假设损失函数
- 为了保证
, 我们选择让 与梯度 的方向相反。最简单的选择是让
正比于梯度的负方向: - 其中,
是一个正的常数,称为学习率 (learning rate) 或步长 (step size)。学习率控制着每次迭代中参数更新的幅度。 - 将
代入 , 得到参数的更新公式: - 这个公式表示在每次迭代中,我们都沿着当前点
处梯度 的反方向移动一小步 (步长为 ), 从而更新参数到 , 希望能够逐步接近损失函数的最小值
误差反向传播 Error Back Propagation (BP)
BP 算法是一种将输出层误差反向传播给隐藏层进行参数更新的方法
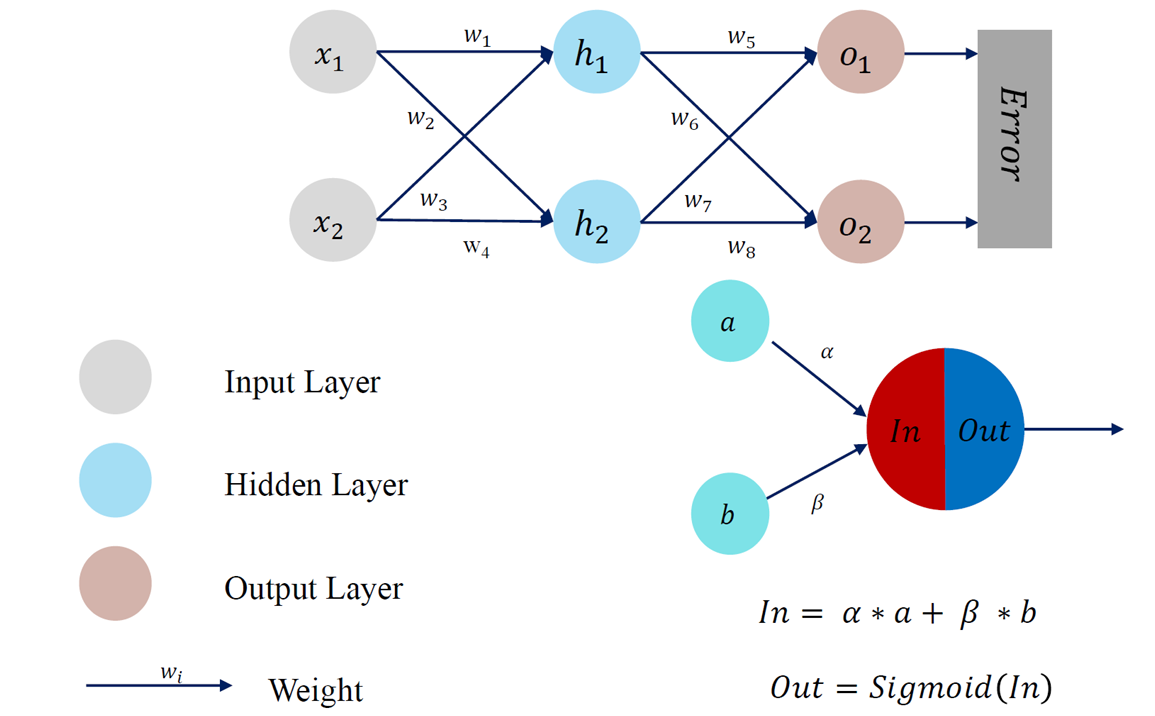
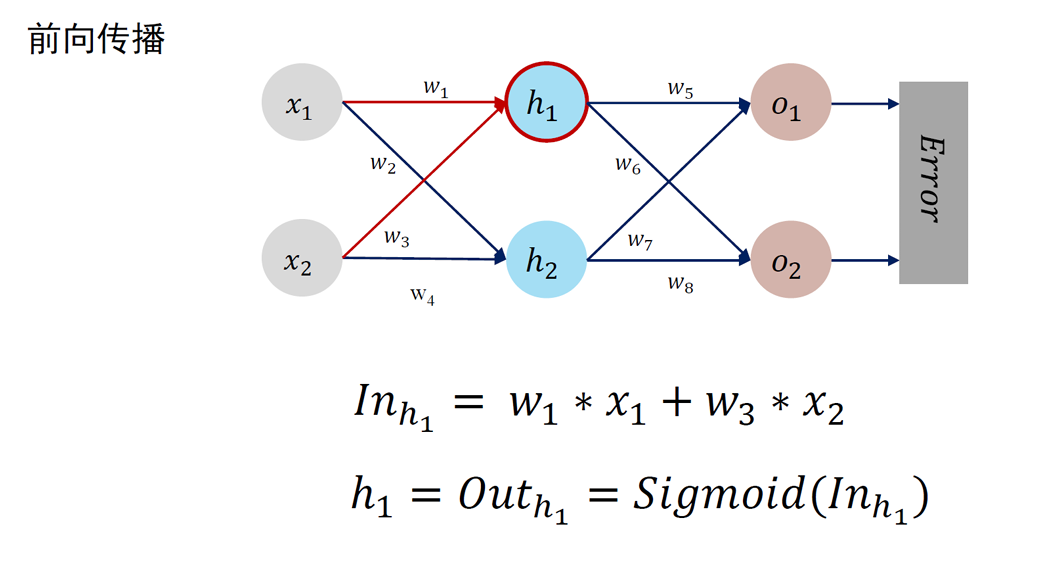
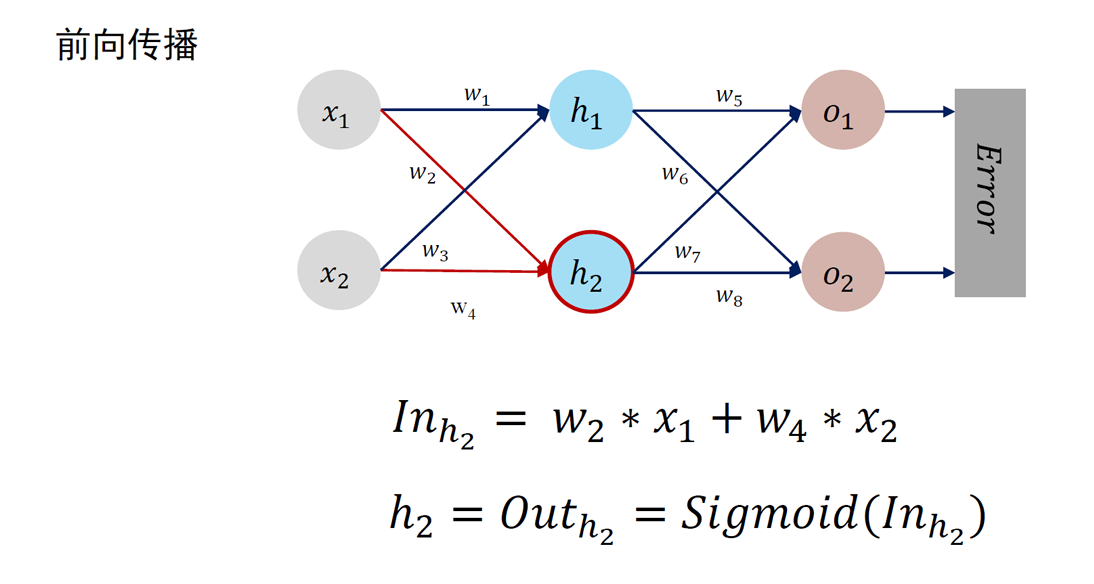
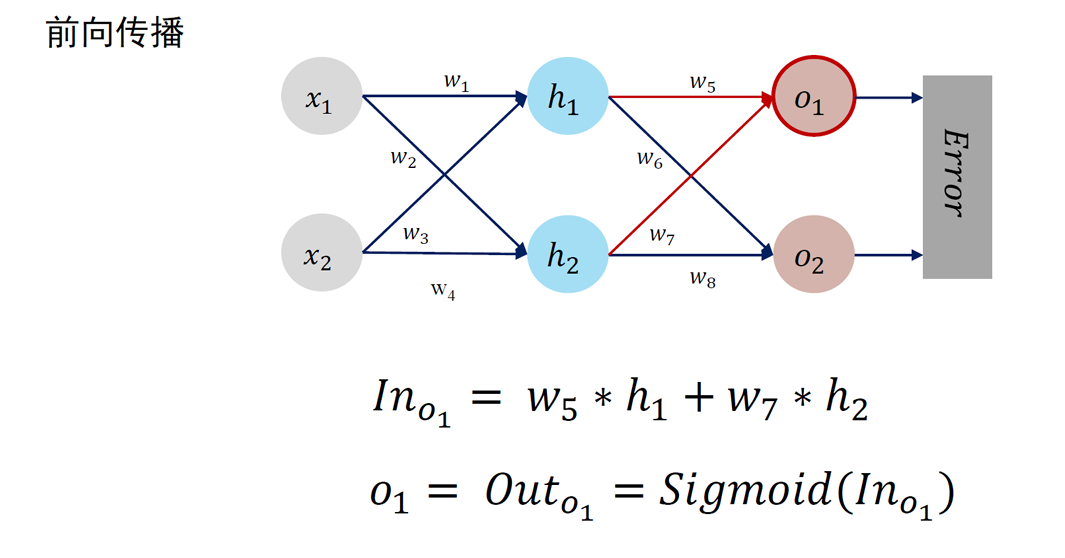
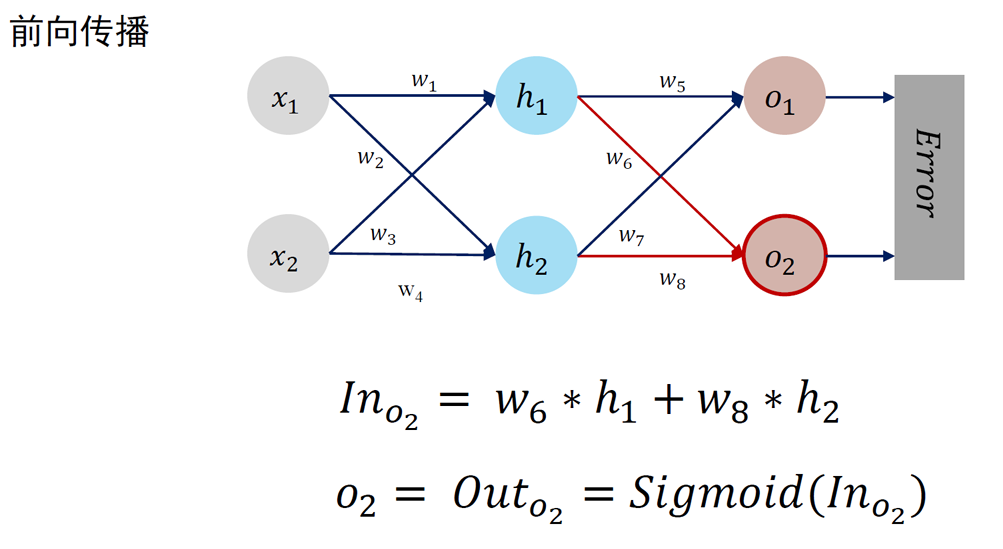
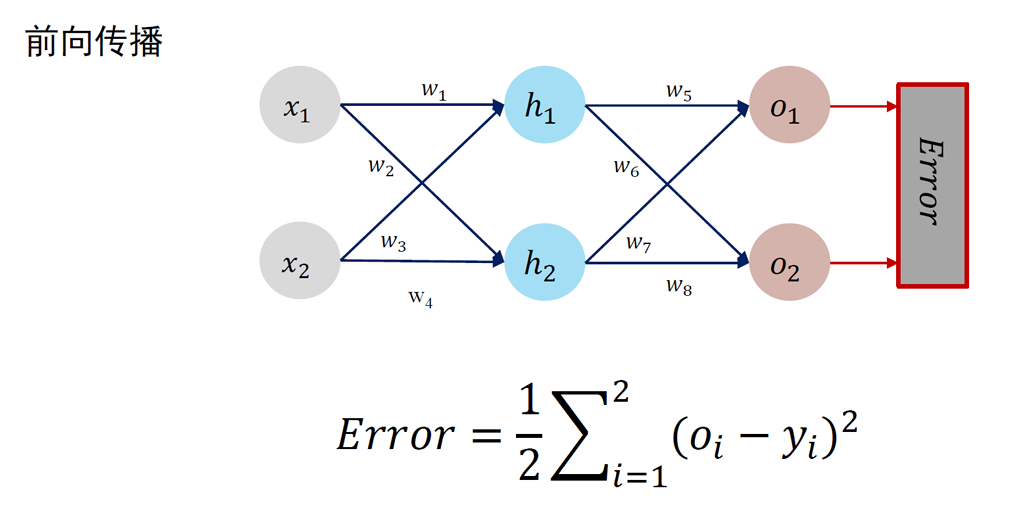
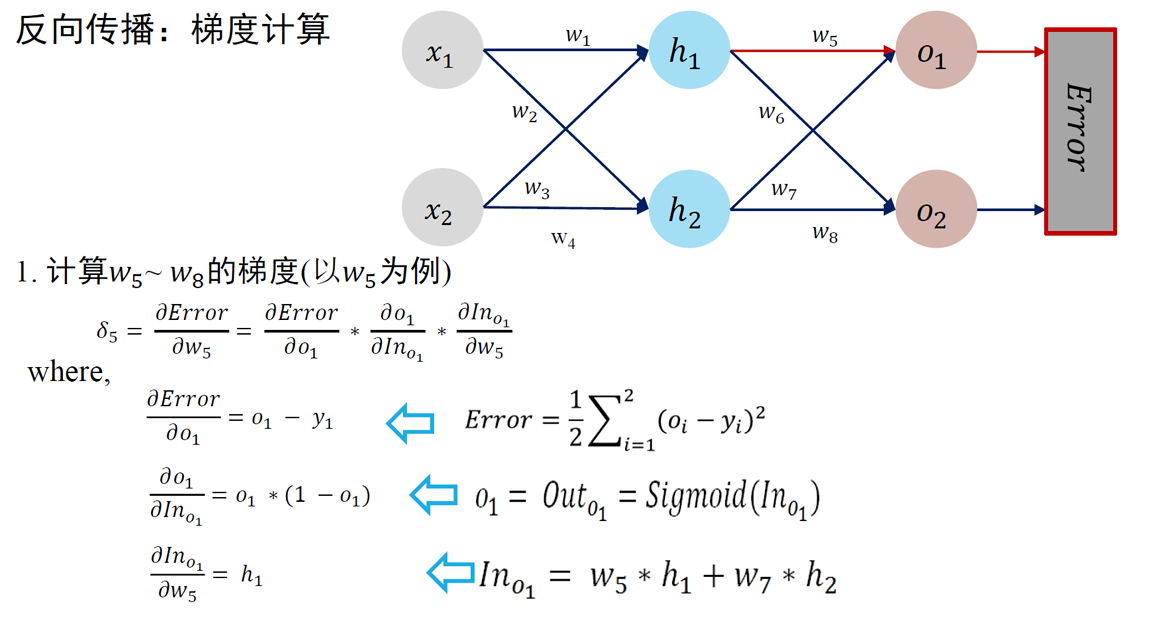
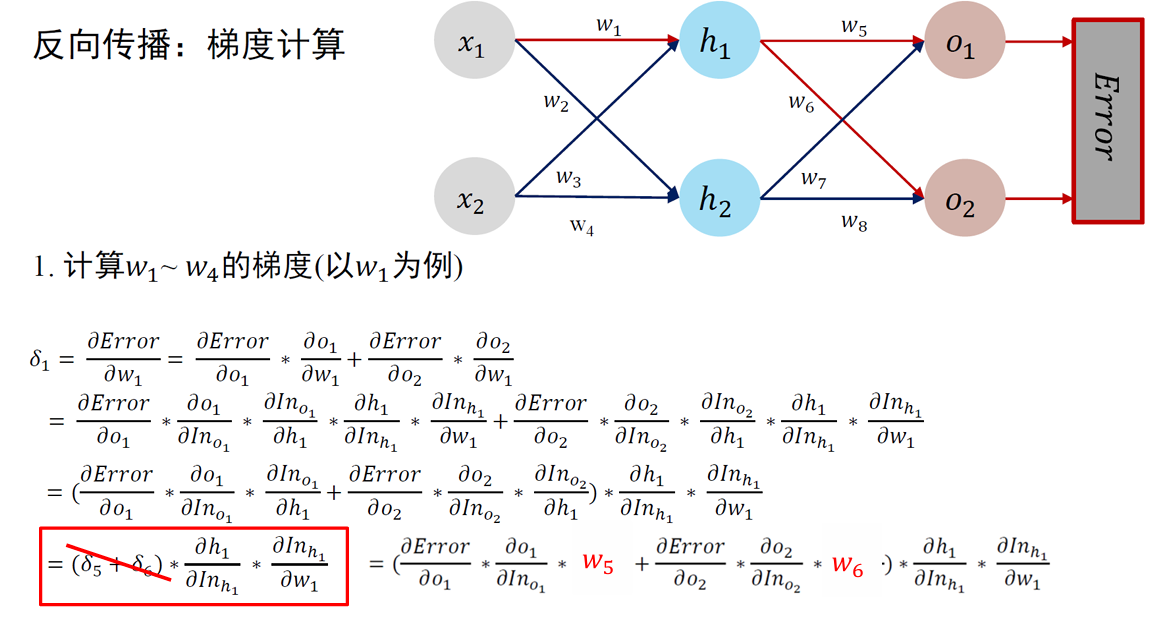
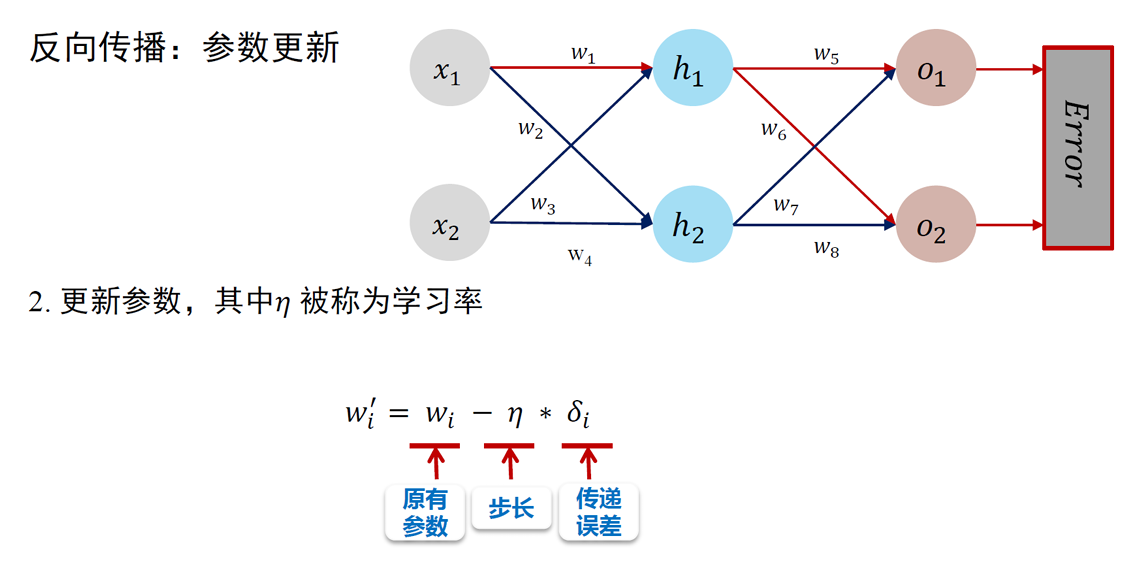
梯度下降算法
- 批量梯度下降(Batch Gradient Descent, BGD)
- 一次迭代对所有样本进行计算,利用矩阵进行操作可实现并行
- 当目标函数为凸函数时,BGD 一定能够得到全局最优
- 当样本数目很大时,每迭代一步都需要对所有样本计算,训练过程会很慢
- 随机梯度下降(Stochastic Gradient Descent,SGD)
- 在每轮迭代中,随机优化一个样本的损失,每一轮参数的更新速度大大加快
- 准确度下降。即使目标函数为强凸函数,SGD 仍无法线性收敛
- 可能会收敛到局部最优,由于单个样本不能代表全体样本趋势
- 不易于实现并行
- 小批量梯度下降(Mini-Batch Gradient Descent, MBGD)
- 每次迭代使用 batch_size 个样本来对参数进行更新
- 目前最常用
在合理地范围内,增大 batch size 的好处:
- 内存利用率提高了
- 跑完一次 epoch (全数据集) 所需的迭代次数减少
- 在一定范围内,一般来说 Batch_Size 越大,其确定的下降方向越准,引起训练震荡越小
盲目增大 batch_size 的坏处:
- 内存容量可能撑不住了
- 跑完一次 epoch (全数据集) 所需的迭代次数减少,但要想达到相同的精度,其所花费的时间大大增加了,从而对参数的修正也就显得更加缓慢
- Batch Size 增大到一定程度,其确定的下降方向已经基本不再变化
4.2 卷积神经网络
为什么需要卷积神经网络👇
当模型参数数量变得巨大时,不仅会占用大量计算机内存,同时也使神经网络模型变得难以训练收敛。因此,对于图像这样的数据,不能直接将所构成的像素点向量与前馈神经网络神经元相连
卷积
- 卷积(convolution):就是针对像素点的空间依赖性来对图像进行处理的一种技术
- 卷积核(kernel):一个二维矩阵 (可以是多维的,例如 RGB 图像,有三维的卷积核,分别针对三个通道进行 convolution)
- 权重:通过数据驱动机制学习得到,捕捉图像空间特征
- 卷积操作:
- 填充 padding:卷积后的图像分辨率与原图一致 → "VALID" 方法
- 否则,会进行下采样 subsampling 👉 “SAME” 方法
- 步长 Stride:每进行一次卷积计算后,卷积核移动的格数
- 填充 padding:卷积后的图像分辨率与原图一致 → "VALID" 方法
- 感受野(receptive field):感受野是特征图上一个点对应输入图像上的区域
- 特征图:卷积滤波结果
- 局部感知,参数共享
- 特征选择性
不同卷积核可被用来刻画视觉神经细胞对外界信息感受时的不同选择性:
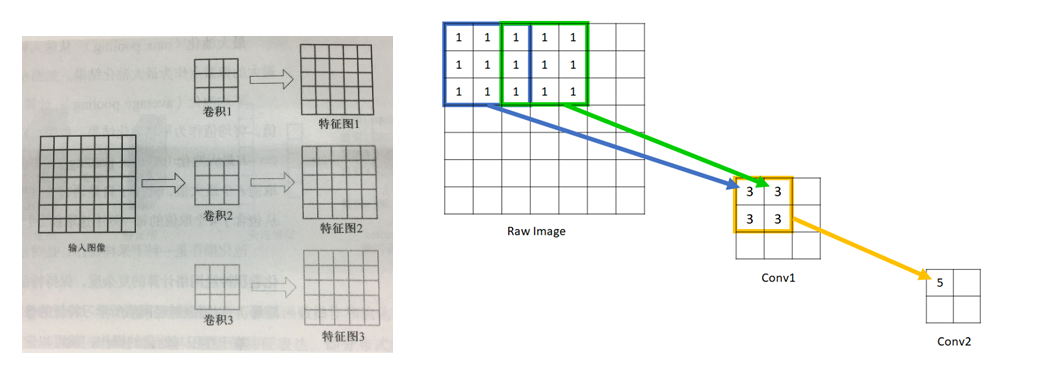
下采样约减抽象:假设被卷积图像大小为
上面的公式是采用了 Padding 策略的,如果不采用 Padding 策略:
池化
图像中存在较多冗余,可用某一区域子块的统计信息 (如最大值或均值等)来刻画该区域中所有像素点呈现的空间分布模式
池化 Pooling: 对输入的特征图进行下采样,以获得最主要的信息
- Max Pooling
- Mean Pooling
- k-max Pooling
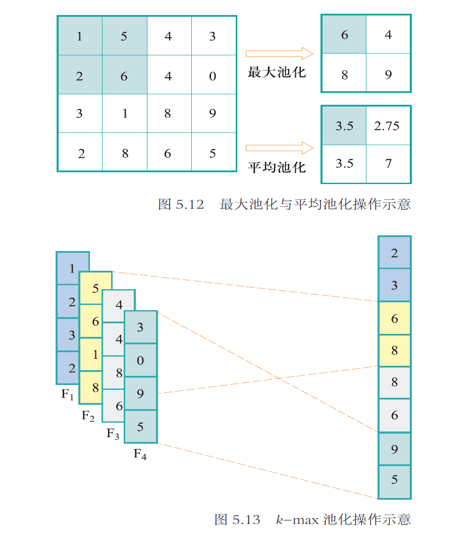
分布式向量表达 (distributed vector representation):卷积神经网络在若干次卷积操作、接着对卷积所得结果进行激活函数操作和池化操作下,最后通过全连接层来学习得到输入数据的特征表达
- 卷积层:提取局部特征
- 池化层:降维
- 激活函数:非线性化
- 全连接层:用于输出想要的结果 (下游任务)
4.3 循环神经网络
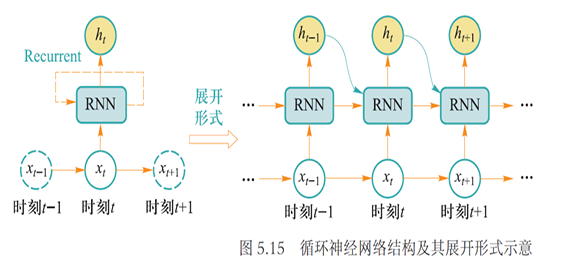
循环神经网络:一类处理序列数据(如文本句子、视频帧等)时所采用的网络结构
- 本质是希望模拟人所具有的记忆能力,在学习过程中记住部分已经出现的信息,并利用所记住的信息影响后续结点输出
基本架构
在时刻
$$h_t=\Phi (\mathrm{U}\times x_t+\mathrm{W}\times h_{t-1})$$
- 这里
是激活函数,一般可为 Sigmoid 或者 Tanh 激活函数,使模型能够忘掉无关的信息,同时更新记忆内容。U 与 W 为模型参数
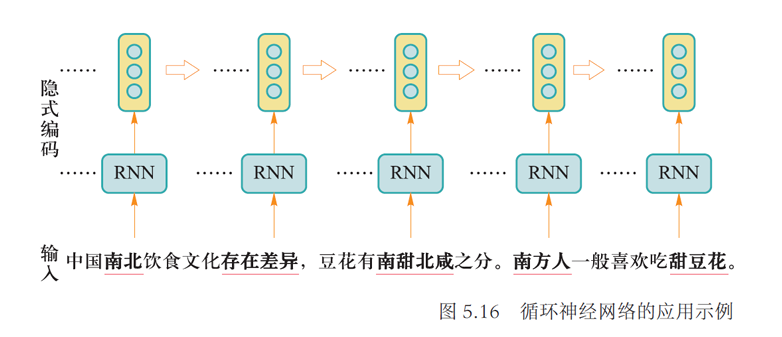
循环神经网络读入每个单词后,先产生对应单词的隐式编码,再如下得到一个句子的向量编码:
- 最后一个单词输出作为整个句子的编码
- 因为句子中所有单词的信息均被后向传递
- 将每个单词的隐式编码进行加权平均,将加权平均结果作为整个句子的向量编码表示
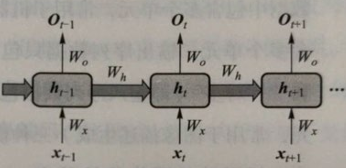
梯度传递
- 时刻
输入数据 (文本中的单词) 的隐式编码为 、其真实输出为 (单词词性)、模型预测 的词性是 - 参数
将 映射为隐式编码 、参数 将 映射为预测输出 、 通过参数 参与 的生成。 - 图中
、 和 是复用参数
假设时刻
LSTM
由于 tanh 函数的导数取值位于 0 到 1 区间,对于长序列而言,若干多个 0 到 1 区间的小数相乘,会使得参数求导结果很小,引发梯度消失问题。为了缓解梯度消失问题,长短时记忆模型(LongShort-Term Memory,LSTM)被提出
引入内部记忆单元和门
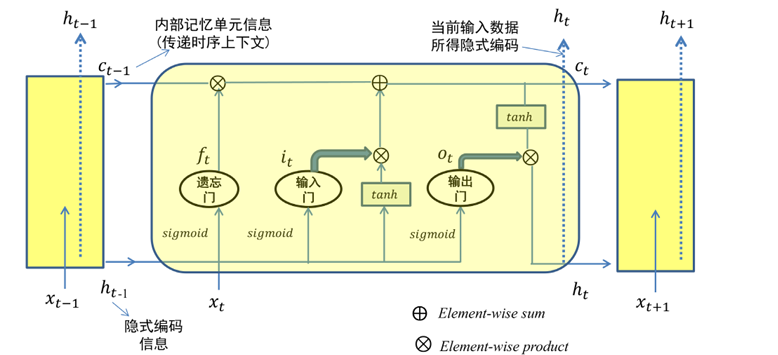
| 符号 | 内容描述/操作 |
|---|---|
| 时刻 t 输入的数据 | |
| 输入门的输出: ( 输入门 |
|
| 遗忘门的输出: ( 遗忘门控制上一时刻内部记忆单元 |
|
| 输出门的输出: ( 输出门控制 |
|
| 内部记忆单元的输出: |
|
| 时刻 $$h_{t}=o_{t}\odot\tanh (c_{t})=o_{t}\odot\tanh (f_{t}\odot c_{t-1}+i_{t}\odot\tanh (W_{xc}x_{t}+W_{hc}h_{t-1}+b_{c}))$$ (输入门、遗忘门和输出门的信息 |
|
| 两个向量中对应元素按位相乘 (element-wise product) 如: |
一些细节:
- 三种门结构的输出
、 和 值域为 - 每个时刻 t 只有
作为本时刻的输出以用于分类等处理 - 实际上,在每个时刻
中只有内部记忆单元信息 和隐式编码 这两种信息起到了对序列信息进行传递的作用
- 实际上,在每个时刻
- LSTM 如何克服梯度消失?
- LSTM 通过引入门结构,在从 t 到 t+1 过程中引入加法来进行信息更新,避免了梯度消失问题
4.4 注意力机制与正则化
注意力机制
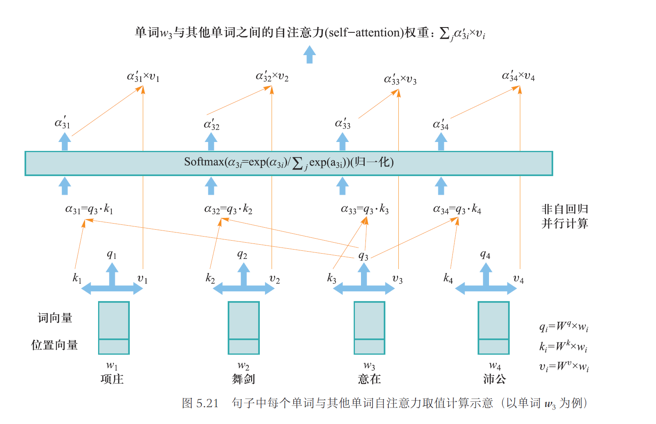
首先生成每个单词的内嵌向量(包含了单词在句子中位置编码向量信息),记为
- 查询向量:
👉 用于搜索的单词 - 键向量:
👉 被搜索物品的描述信息 (例如标题) - 值向量:
👉 被搜索物品实际的语义内容 - 后面可以看到,对每个单词而言
, 、 和 三个映射矩阵都是一样的,也是自注意力模型需要训练的全部参数 - 自注意力模型就是要挖掘单词
与其他单词在句子中因为上下文(context)关联而具有的自注意力取值大小
以图 5.21 中单词
- 计算
所对应查询向量与其他单词键向量之间的点积,该点积可作为单词 与其他单词之间的关联度: - 对
结果通过 softmax 函数进行归一化操作,得到 。对于给定“项庄舞剑、意在沛公”句子, 记录了“意在”单词与其他单词所具有的重要程度(即注意力) 乘以每个单词 所对应的值向量 ,即 - 对上一步结果进行
,这个结果作为在当前句子语境下单词 “注意”到与其他单词的关联程度(self-attention)
正则化
正则化系数 👉 缓解神经网络在训练过程中出现的过拟合问题
有如下几种方法:
- Dropout
每次参数更新时随机丢掉一部分神经元来减少神经网络复杂度,防止过拟合 - Batch-Normalization(批归一化)
通过规范化的手段,把神经网络每层中任意神经元的输入值分布改变到均值为 0、方差为 1 的标准正态分布 - L1-Norm & L2-Norm
范数:数学表示为 , 指模型参数 中各个元素的绝对值之和
范数也被称为 “稀疏规则算子” ( Lasso regularization)
范数:数学表示为 , 指模型参数 中各个元素平方和的开方
"结构风险最小化"
4.5 自然语言和计算机视觉应用
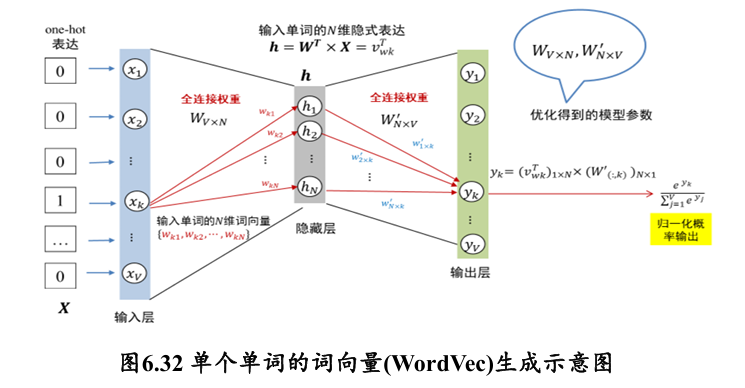
如何获得单个单词的词向量?
- 将该单词表示成
维 one-hot 向量 - 隐藏层神经元大小为
, 每个神经元记为 - 向量
中每个 与隐藏层神经元是全连接,连接权重矩阵为 - 这里
和 为模型参数 - 一旦训练得到了下图的神经网络,就可以将输入层中
与隐藏层连接权重为 (隐藏层) 作为第 个单词 维词向量 (word vector)
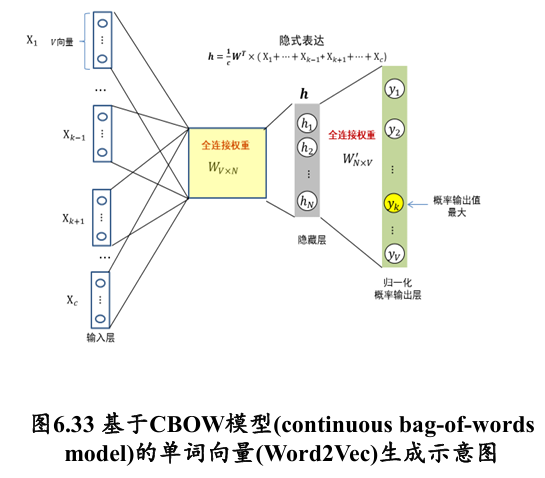
Continuous Bag-of-Words (CBoW):根据某个单词所处的上下文单词来预测该单词
可用
- 每个输入单词仍然是
维向量(可以是 one-hot 的表达) - 隐式编码为每个输入单词所对应编码的均值
Skip-gram:利用某个单词来分别预测该单词的上下文单词
无论是 CBOW 还是 Skip-Gram 模式,随着单词个数数目增加,模型参数数目也迅速上升
👉 加快模型训练:层次化 Softmax(Hierarchical Softmax)与负采样(Negative Sampling)
05 强化学习
- 价值函数 V 与动作-价值函数 q 之间的关系:
- 贝尔曼方程 (Bellman Equation) 也被称作动态规划方程
- 价值函数的贝尔曼方程:
- 动作-价值函数的贝尔曼方程:
- 价值函数的贝尔曼方程:
- 强化学习的求解方法:
- 基于价值方法 (value-based)
- 通过策略计算价值函数的过程叫做策略评估 (policy evaluation)
① 动态规划 (Dynamic Programming, DP):
② 蒙特卡洛采样 (Monte Carlo Sampling, MC):
③ 时序差分 (Temporal Difference, TD): - 通过价值函数优化策略的过程叫做策略优化 (policy improvement)
- 策略评估和策略优化交替进行的强化学习求解方法叫做通用策略迭代 (Generalized Policy Iteration, GPI)
- 策略优化定理 (Policy Improvement Theorem)
- 价值迭代 (value iteration) 算法: 在策略评估动态规划法的基础上, 每次迭代只对一个状态进行策略评估和策略优化
- Q 学习算法: 直接记录和更新动作-价值函数
而不是价值函数 , Q 学习中, 只有动作-价值函数 (即 q 函数) 参与计算。 - 在 Q 学习中引入探索与利用机制, 用 e 贪心 (e-greedy) 策略来代替
: 增大 e 值能促进算法探索 - 深度强化学习方法 DQN: 将动作-价值函数参数化
- 在 Q 学习中引入探索与利用机制, 用 e 贪心 (e-greedy) 策略来代替
- 通过策略计算价值函数的过程叫做策略评估 (policy evaluation)
- 基于策略 (policy-based): 策略梯度法、策略梯度定理、REINFORCE (基于蒙特卡洛采样的策略梯度法)、Actor-Critic 算法
- 基于模型 (model-based)
- 基于价值方法 (value-based)
5.1 强化学习定义
在智能主体与环境的交互中,学习能最大化收益的行动模式:
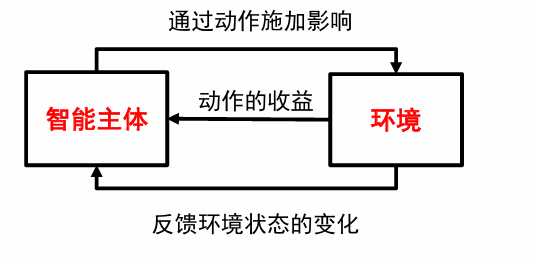
- 智能体(agent):强化学习算法的主体,根据经验做出主观判断并执行动作
- 环境(environment):智能体以外的一切统称为环境,环境在与智能体的交互中,能被智能体所采取的动作影响,同时环境也能向智能体反馈状态和奖励
- 状态(state):智能体对环境的一种理解和编码,通常包含了对智能体所采取决策产生影响的信息
- 动作(action):智能体对环境产生影响的方式
- 策略(policy):智能体在所处状态下去执行某个动作的依据,即给定一个状态,智能体可根据一个策略来选择应该采取的动作
- 奖励(reward):智能体序贯式采取一系列动作后从环境获得的收益
三种学习方式对比:
| 学习方式 | 学习依据 | 数据来源 | 决策过程 | 学习目标 |
|---|---|---|---|---|
| 监督学习 | 基于监督信息 | 一次给定 | 单步决策(如分类和识别等) | 样本到语义标签的映射 |
| 无监督学习 | 基于对数据结构的假设 | 一次给定 | 无 | 数据的分布模式 |
| 强化学习 | 基于评估 | 在时序交互中产生 | 序贯决策(如棋类博弈) | 选择能够获取最大收益的状态到动作的映射 |
离散马尔可夫过程 Discrete Markov Process
基本概念
随机过程:是一列随时间变化的随机变量;
- 当时间是离散量时,一个随机过程可以表示为
, 其中每个 都是一个随机变量,这被称为离散随机过程
马尔可夫链(Markov Chain):满足马尔可夫性(Markov Property)的离散随机过程,也被称为离散马尔科夫过程
- 𝒕+𝟏时刻状态仅与𝒕时刻状态相关
- 二阶:𝒕 +𝟏时刻状态与𝒕和𝒕−𝟏时刻状态相关
马尔可夫奖励过程(Markov Reward Process):引入奖励
- 奖励函数
, 其中 描述了从第 步状态转移到第 步状态所获得奖励 - 在一个序列决策过程中,不同状态之间的转移产生了一系列的奖励
, 其中 为 的简便记法 - 为了比较不同的奖励序列,定义反馈 (return), 用来反映累加奖励:
其中衰退系数 (decay factor)
马尔可夫决策过程(Markov Decision Process):引入动作
- 定义智能主体能够采取的动作集合为
可以是无限的 - 由于不同的动作对环境造成的影响不同,因此状态转移概率定义为
,其中 为第 步采取的动作
可以是随机概率性的转移 - 奖励可能受动作的影响,因此修改奖励函数为

使用离散马尔可夫决策过程描述机器人移动问题:
- 随机变量序列
: 表示机器人第 步所在位置(即状态),每个随机变量 的取值范围为 - 动作集合:
- 状态转移概率
: 满足马尔可夫性,其中 。状态转移 - 奖励函数:
- 衰退系数:
综合以上信息,可通过
- 马尔可夫决策过程
是刻画强化学习中环境的标准形式 - 马尔可夫决策过程可用如下序列来表示:
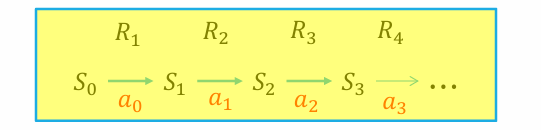
- 马尔科夫过程中产生的状态序列称为轨迹 (trajectory), 可如下表示
- 轨迹长度可以是无限的,也可以有终止状态
。有终止状态的问题叫做分段的 (episodic), 否则叫做持续的 (continuing) - 分段问题中,一个从初始状态到终止状态的完整轨迹称为一个片段 (episode)
策略学习
智能主体如何与环境交互而完成任务?需要进行策略学习
- 已知的:S A R
- 不一定已知的:Pr
- 观察到的:
策略函数:
- 策略函数
, 其中 的值表示在状态 s 下采取动作 的概率 - 策略函数的输出可以是确定的,即给定 s 情况下,只有一个动作
使得概率 s, 取值为 1。对于确定的策略,记为
为了对策略函数𝜋进行评估,定义
- 价值函数 (Value Function)
, 其中
即在第步状态为 s 时,按照策略 行动后在未来所获得反馈值的期望 - 动作-价值函数 (Action-Value Function)
, 其中
表示在第步状态为 s 时,按照策略 采取动作 后,在未来所获得反馈值的期望
这样,策略学习转换为如下优化问题:寻找一个最优策略
价值函数的贝尔曼方程:
- 当前状态价值函数等于瞬时奖励的期望加上后续状态的(折扣)价值函数的期望
- 价值函数取值与时间没有关系,只与策略π、在策略π下从某个状态转移到其后续状态所取得的回报、以及在后续所得回报有关
动作-价值函数的贝尔曼方程:
- 当前状态下的动作-价值函数等于瞬时奖励的期望加上后续状态的(折扣)动作-价值函数的期望
5.2 基于价值的强化学习
强化学习求解:在策略优化和策略评估的交替迭代中优化参数

策略评估和策略优化交替进行的强化学习求解方法叫做通用策略迭代
- 策略评估:通过策略计算价值函数
- 策略优化:根据价值函数更新策略
策略优化
给定当前策略

策略评估
通过迭代计算贝尔曼方程进行策略评估
- 动态规划
- 蒙特卡洛采样
- 时序差分(Temporal Difference)
动态规划
- 初始化
函数 - 循环
- 枚举
- 枚举
策略评估的时候,我们主要更新价值函数的值;再在策略优化的时候,更新价值-动作函数的值,从而更新策略
目前的策略,是在 s1 时采取"上"的策略

缺点:智能主体需要事先知道状态转移概率;无法处理状态集合大小无限的情况
蒙特卡洛采样
给定状态 s,从该状态出发不断采样后续状态,得到不同的采样序列。通过这些采样序列来分别计算状态 s 的回报值,对这些回报值取均值,作为对状态 s 价值函数的估计,从而避免对状态转移概率的依赖
- 选择不同的起始状态,按照当前策略
采样若干轨迹,记它们的集合为 D - 枚举
- 计算
中 s 每次出现时对应的反馈
- 计算
利用公式:$$G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdots $$

时序差分
可以看作蒙特卡罗方法和动态规划方法的有机结合
- 从实际经验中获取信息,无需提前获知环境模型的全部信息
- 利用前序已知信息来进行在线实时学习,无需等到整个片段结束(终止状态抵达)再进行价值函数的更新
使用下一时刻状态的价值函数来估计当前状态的价值函数,而不是使用整个片段的反馈值
- 初始化
函数 - 循环
- 初始化 s 为初始状态
- 循环
动作 a 的选取服从策略分布 - 执行动作
, 观察奖励 和下一个状态 - 更新
- 直到 s 是终止状态
- 直到
收敛

时序差分法和蒙特卡洛法都是通过采样若干个片段来进行价值函数更新的,但是时序差分法并非使用一个片段中的终止状态所提供的实际回报值来估计价值函数,而是根据下一个状态的价值函数来估计,这样就克服了采样轨迹的稀疏性可能带来样本方差较大的不足问题,同时也缩短了反馈周期
基于价值的强化学习算法
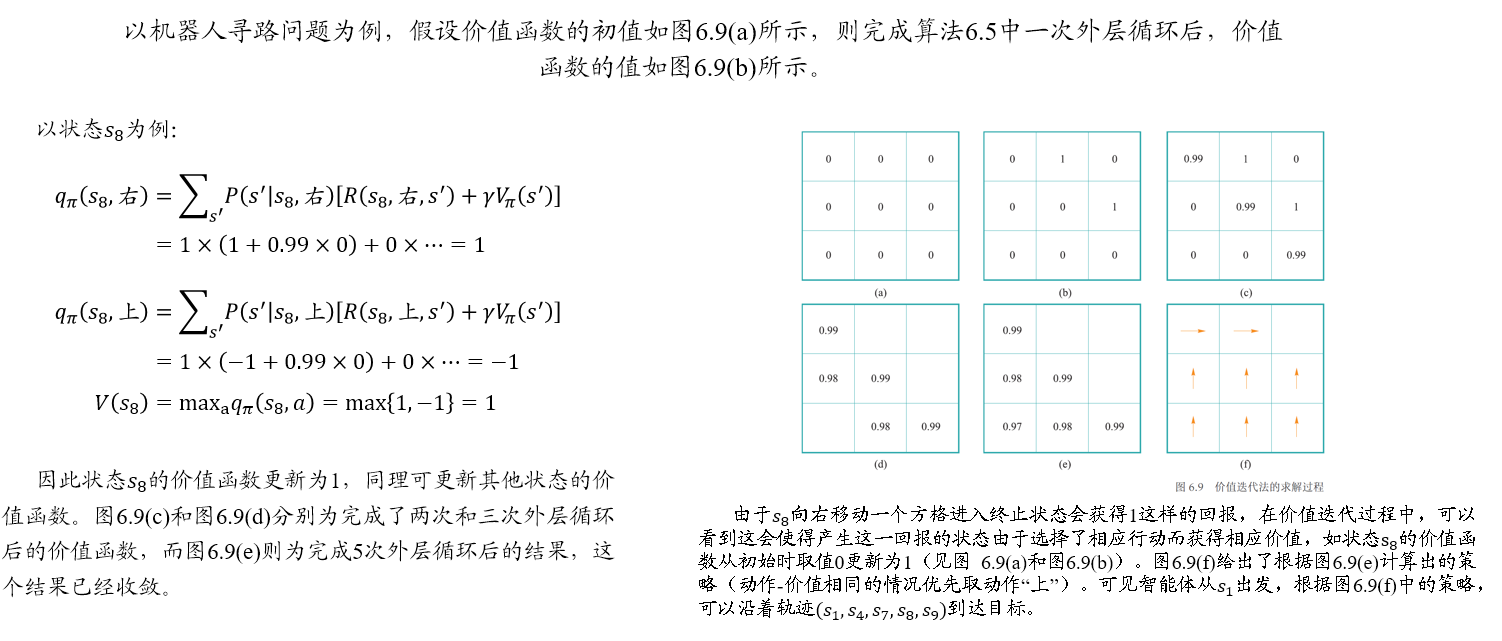
结合策略优化和策略评估两个阶段,得到基于价值的强化学习算法:在策略评估动态规划法的基础上, 每次迭代只对一个状态进行策略评估和策略优化
注意这里不涉及时序差分中的
- 随机初始化
- repeat
- foreach
do // 这里是 max 函数
- end
- foreach
- until
收敛
Q-Learning
Q 学习中直接记录和更新动作-价值函数
- 初始化
函数 - 循环
- 初始化 s 为初始状态
- 循环
- 执行动作
, 观察奖励 和下一个状态 - 更新
- 直到 s 是终止状态
- 直到
收敛

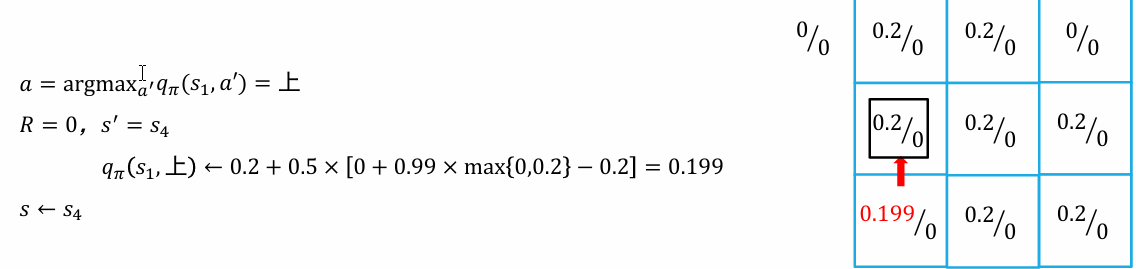
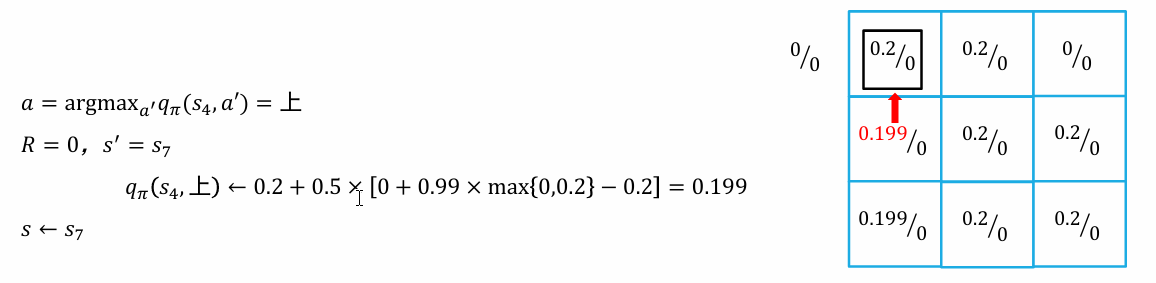

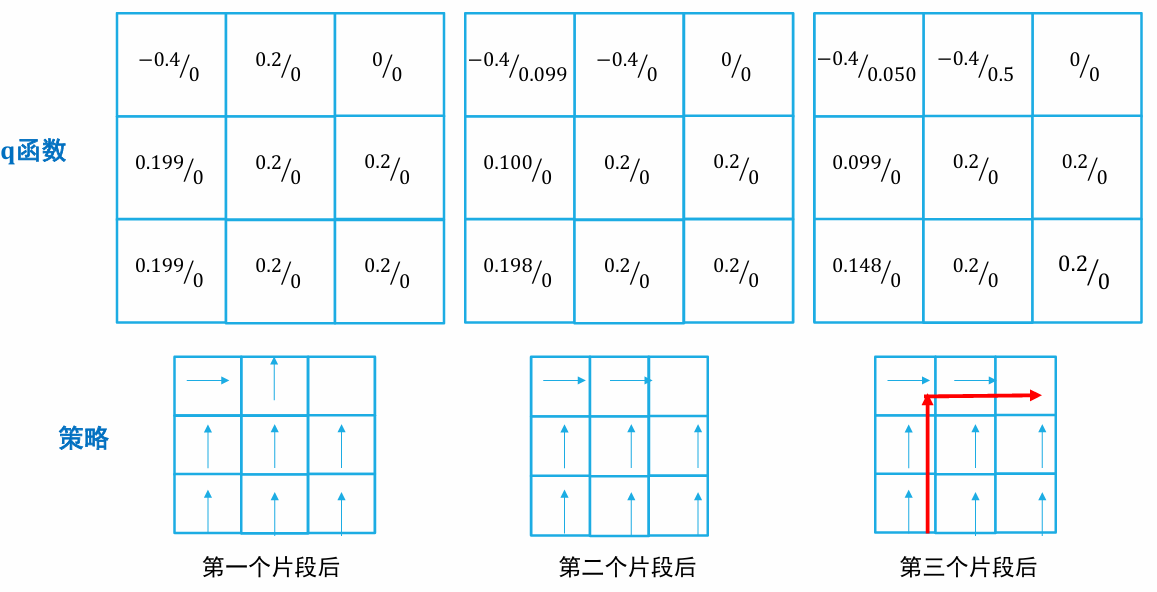
探索(exploration)与利用(exploitation)的平衡
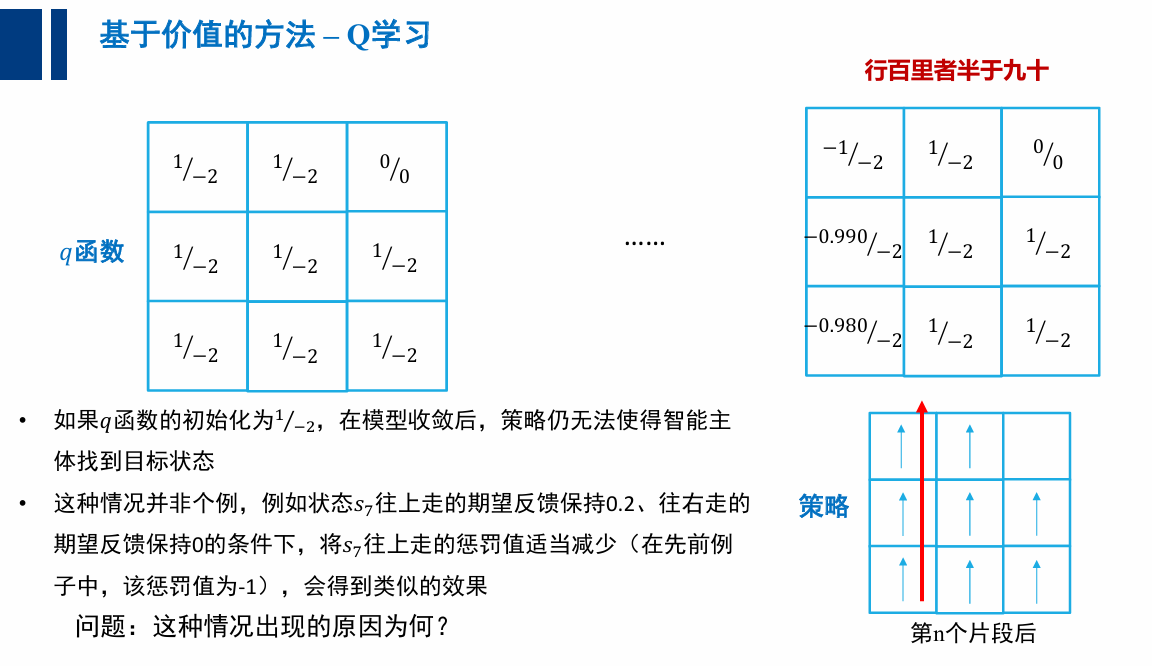
为何 Q 学习收敛到非最优策略?
- 算法中只有利用没有探索
- (特定的 q 初始 q 函数,会让策略无法改变其轨迹)
大体上利用,偶尔探索👇
- 初始化
函数 - 循环
- 初始化 s 为初始状态
- 循环
- 执行动作
, 观察奖励 和下一个状态 - 更新
- 直到 s 是终止状态直到
收敛
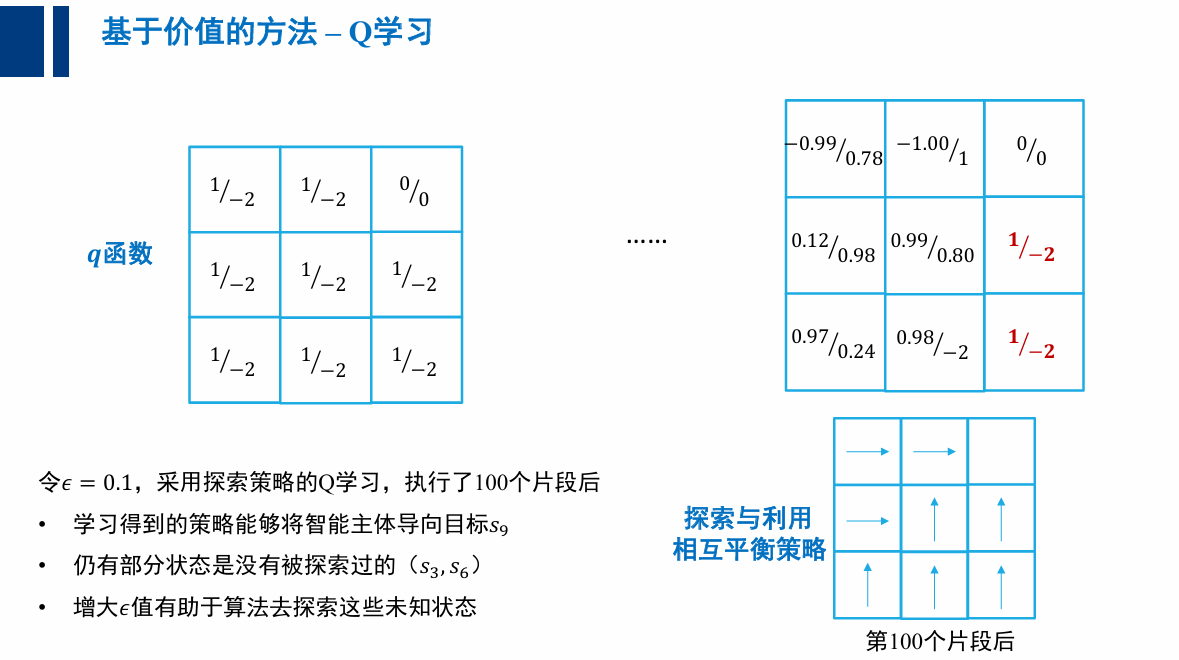
参数化与深度强化学习
- 状态数量太多时,有些状态可能始终无法采样到
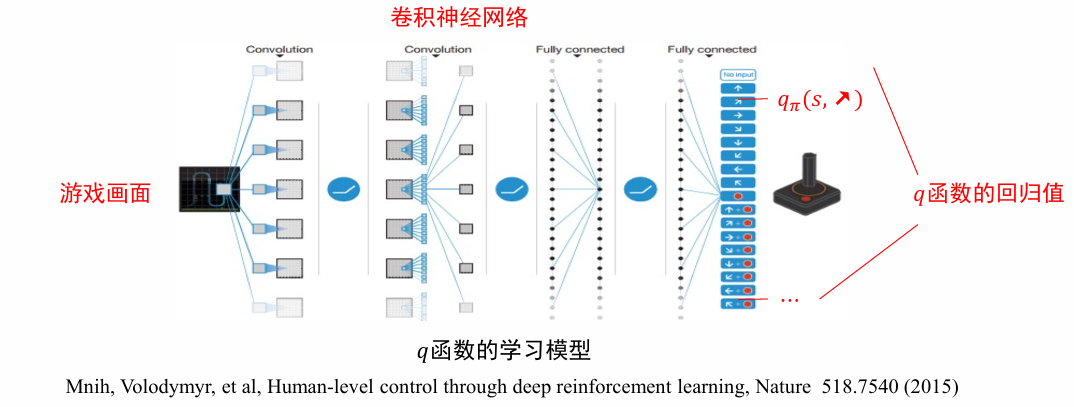
- 状态数量无限时,不可能用一张表 (数组) 来记录𝑞函数的值
👉 将𝑞函数参数化(parametrize),用一个非线性回归模型来拟合𝑞函数,例如 (深度) 神经网络

- 初始化
函数的参数 - 循环
- 初始化 s 为初始状态
- 循环
- 采样
- 执行动作
, 观察奖励 和下一个状态 s' - 损失函数 L
- 根据梯度
更新参数
- 采样
- 直到 s 是终止状态
- 指导
收敛
两个不稳定因素:
- 相邻的样本来自同一条轨迹,样本之间相关性太强,集中优化相关性强的样本可能导致神经网络在其他样本上效果下降 👉 采样不足
- 在损失函数中,𝑞函数的值既用来估计目标值,又用来计算当前值。现在这两处的𝑞函数通过𝜃有所关联,可能导致优化时不稳定 👉 难以收敛
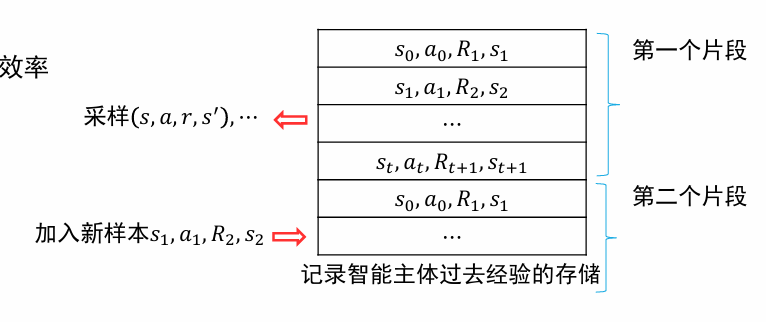
经验重现 Experience Replay
- 将过去的经验存储下来,每次将新的样本加入到存储中去,并从存储中采样一批样本进行优化
- 在算法对参数 θ 进行更新时,则从经验重现表中随机选取一批样本用于计算损失函数
- 解决了样本相关性强的问题
- 重用经验,提高了信息利用的效率
目标网络 Target Network
$$L (\theta)=\frac12[R+\gamma\max_{a^{\prime}}\boxed{q_\pi (s^{\prime}, a^{\prime};\theta^{-})}-q_\pi (s, a;\theta)]^2$$
- 损失函数的两个 𝑞 函数使用不同的参数计算
- 用于计算估计值的
使用参数 计算,这个网络叫做目标网络 - 用于计算当前值的
使用参数 计算 - 保持
的值相对稳定,例如 每更新多次后才同步两者的值
5.3 基于策略的强化学习
通过直接参数化策略函数的方法求解强化学习问题;算法需要求参数化的策略函数的梯度,因此这些方法称为策略梯度法
- 策略函数的参数化可以表示为
,其中θ为一组参数,函数取值表示在状态 s 下选择动作 a 的概率 - 和 Q 学习的ϵ贪心策略相比,选择一个动作的概率是随着参数的改变而光滑变化的,对算法收敛有更好的保证
假设强化学习问题的初始状态为
策略梯度定理
如果能够计算或估计策略函数的梯度,智能体就能直接对策略函数进行优化:
称为策略 的策略分布 (这里假设折扣系数 ) - 在持续问题中,
为算法在策略 安排下从 出发经过无限多步后位于状态 的概率 - 在分段问题中,
为归一化后的算法从 出发访问 s 次数的期望。 - 当
时,则需要给每个状态的 值加上一个权重 - 为了简化说明,下文在进行公式推导时始终假设
- 为了简化说明,下文在进行公式推导时始终假设
基于蒙特卡洛采样的策略梯度法:REINFORCE
- 算法只需根据策略来采样一个状态 s、一个动作 a 和将来的轨迹,就能构造公式中求取期望所对应的一个样本
- 利用采样得到的轨迹片段来估计梯度,并使用梯度上升法来优化策略
基于时序差分的策略梯度法:Actor-Critic 算法
- 使用下一时刻状态的价值函数来估计当前状态的价值函数,而不是使用整个片段的反馈值
- 和 DQN 一致,计算 q 值时使用另一套参数 w 进行计算
5.4 深度强化学习应用
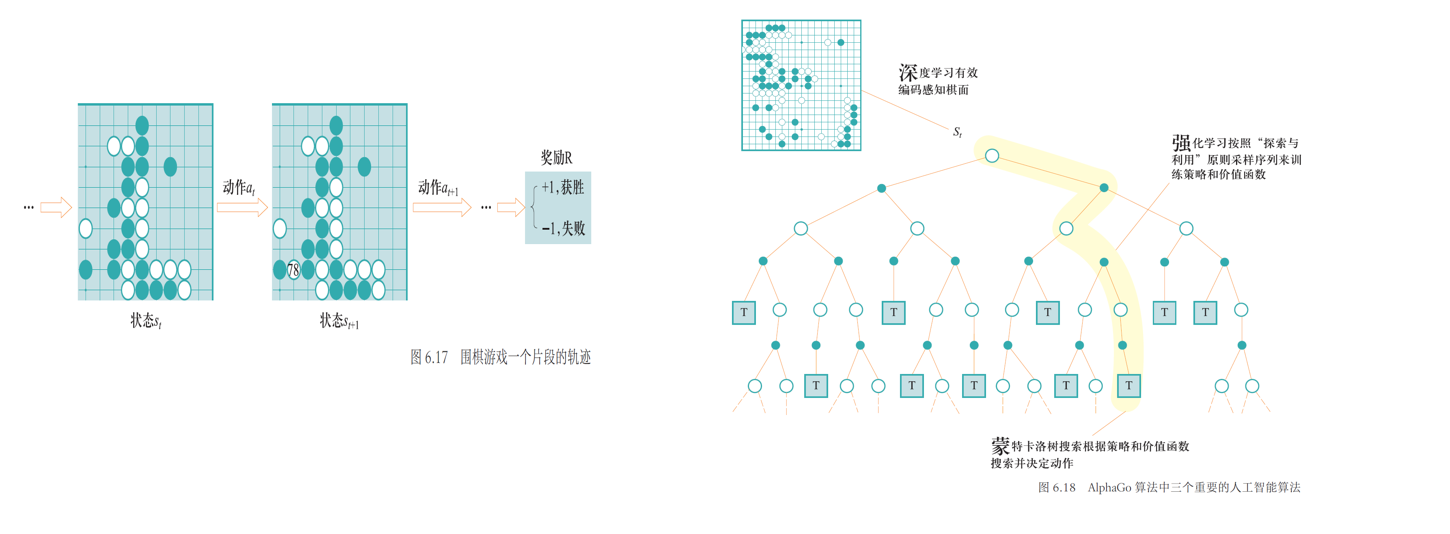
面临的挑战:
- 奖励的设置
- 样本的采集
- 局部最优解与探索
- 训练时的不稳定性与方差
- 泛化和迁移能力
06 人工智能博弈
6.1 博弈论相关概念
博弈行为:带有相互竞争性质的主体,为了达到各自目标和利益,采取的带有对抗性质的行为
- 主要研究博弈行为中最优的对抗策略及其稳定局势
相关概念:
- 参与者或玩家(player):参与博弈的决策主体
- 策略(strategy):参与者可以采取的行动方案,是一整套在采取行动之前就已经准备好的完整方案
- 某个参与者可采纳策略的全体组合形成了策略集(strategy set)
- 所有参与者各自采取行动后形成的状态被称为局势(outcome)
- 如果参与者可以通过一定概率分布来选择若干个不同的策略,这样的策略称为混合策略 (mixed strategy)
- 若参与者每次行动都选择某个确定的策略,这样的策略称为纯策略 (pure strategy)
- 收益(payoff):各个参与者在不同局势下得到的利益
- 混合策略意义下的收益应为期望收益(expected payoff)
- 规则(rule):对参与者行动的先后顺序、参与者获得信息多少等内容的规定
研究范式:建模者对参与者(player)规定可采取的策略集 (strategy sets) 和取得的收益,观察当参与者选择若干策略以最大化其收益时会产生什么结果
在囚徒困境中,最优解为两人同时沉默,但是两人实际倾向于选择同时认罪(均衡解)

博弈的分类
- 合作博弈与非合作博弈
- 合作博弈(cooperativegame):部分参与者可以组成联盟以获得更大的收益
- 非合作博弈(non-cooperative game):参与者在决策中都彼此独立,不事先达成合作意向
- 静态博弈与动态博弈
- 静态博弈(static game):所有参与者同时决策,或参与者互相不知道对方的决策
- 动态博弈(dynamic game):参与者所采取行为的先后顺序由规则决定,且后行动者知道先行动者所采取的行为
- 完全信息博弈与不完全信息博弈
- 完全信息(complete information):所有参与者均了解其他参与者的策略集、收益等信息
- 不完全信息(incompleteinformation):并非所有参与者均掌握了所有信息
博弈的稳定局势 👉 纳什均衡:如果在一个策略组合上,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡
- Nash 定理:若参与者有限,每位参与者的策略集有限,收益函数为实值函数,则博弈必存在混合策略意义下的纳什均衡
- 囚徒困境中两人同时认罪就是这一问题的纳什均衡



- 归纳法证明即可
6.2 博弈策略求解
遗憾最小化算法
对于一个有 N 个玩家参加的博弈,玩家 i 在博弈中采取的策略记为
- 对于所有玩家来说,他们的所有策略构成了一个策略组合,记作
- 策略组中, 除玩家 i 外,其他玩家的策略组合记作
最优反应策略:
- 给定策略组合
, 玩家 在终结局势下的收益记作 - 在给定其他玩家的策略组合
的情况下,对玩家 i 而言的最优反应策略 满足如下条件: 是玩家 可以选择的所有策略
在策略组合
在有限对手、有限策略情况下,纳什均衡一定存在
此时,策略组
算法定义
遗憾最小化算法是一种根据以往博弈过程中所得遗憾程度来选择未来行为的方法
玩家 i 在过去 T 轮中采取策略
其中
简单地说,累加遗憾值代表着在过去 T 轮中,玩家 i 在每一轮中选择策略
遗憾匹配:
- 获取玩家 𝑖 的所有可选策略的遗憾值
- 根据遗憾值的大小来选择后续第 𝑇+1 轮博弈的策略
定义有效遗憾值:遗憾值为负数的策略 👉 不能提升下一时刻收益
利用有效遗憾值的遗憾匹配可得到玩家
表示玩家 所有策略的总数
依照一定的概率选择行动是为了防止对手发现自己所采取的策略(如采取遗憾值最大的策略)
问题描述:假设两个玩家 A 和 B 进行石头-剪刀-布(Rock-Paper-Scissors,RPS)的游戏,获胜玩家收益为 1 分,失败玩家收益为-1 分,平局则两个玩家收益均为零分
第一局时,若玩家 A 出石头(R),玩家 B 出布(P),则此时玩家 A 的收益
- 对于玩家 A ,在玩家 B 出布(P)这个策略情况下,如果玩家 A 选择出布(P)或者剪刀(S),则玩家 A 对应的收益值
或者 - 即 T = 1 时
- 布策略遗憾值:
- 剪刀策略遗憾值:
- 布策略遗憾值:
- 即 T = 1 时
- 对于玩家 B,在玩家 A 出石头 (R) 这个策略情况下
- 即 T = 1 时
- 石头策略遗憾值:
- 剪刀策略遗憾值:
- 石头策略遗憾值:
- 即 T = 1 时
在第二局中:
- 玩家 A 选择石头、剪刀和布这三个策略的概率分别为 0、2/3、1/3
- 玩家 B 的有效遗憾值积累小于 0,所以随机选择策略
假设玩家 A 在第二局按照遗憾值最大的策略选择“剪刀”、玩家 B 随机选择“石头”,计算得到玩家 A 的累加遗憾值:
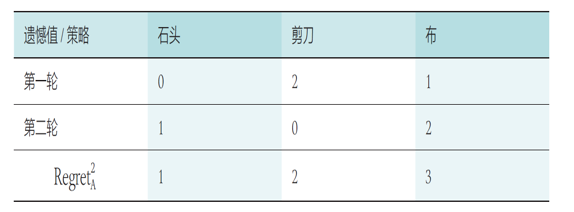
在第三局时,玩家 A 选择“石头”、“剪刀”和“布”的概率分别为 1/6 、 2/6(1/3)、 3/6(1/2)。
需要注意的是,玩家 A 既可以按照遗憾值最小在第三轮来选择“布”这一策略,又可以随机选择“石头”或“剪刀”以防止自己的策略被对手察觉
虚拟遗憾最小化算法
很多博弈(围棋、扑克)需要多次决策才能判断胜负,会导致博弈状态空间呈指数增长时,对一个规模巨大的博弈树无法采用最小遗憾算法,因此需要采取虚拟遗憾最小化算法(counterfactual regret minimization)
也就是说,一轮代表着多次决策,多次决策才能达到终局
算法理论
对于任何序贯决策的博弈对抗,可将博弈过程表示成一棵博弈树
- 每一个中间节点都是一个信息集 I,包含博弈中当前的状态
- 给定博弈树的一个节点,可以从一系列的动作中选择一个,然后状态发生转换,如此周而复始,直到终局(博弈树的叶子节点)
- 玩家在当前状态下可采取的策略就是当前状态下所有可能动作的一个概率分布
具体而言,在信息集 I 下,玩家可以采取的行动集合记作
- 玩家 i 所采取的行动
可认为是其采取的策略 的一部分 - 在信息集 I 下采取行动 a 所代表的策略记为
- 计算虚拟遗憾值的对象:每个中间节点在信息集下所采取的行动
- 然后根据遗憾值匹配,得到该节点在信息集下应该采取的策略
- 然后根据遗憾值匹配,得到该节点在信息集下应该采取的策略
在一次博弈中,所有玩家交替采取的行动序列记为
在策略组合
博弈的终结局势集合也就是博弈树中叶子节点的集合,记为
- 对于任意一个终结局势
,玩家 在此终点局势下的收益记作 - 给定行动序列
,依照策略组合 最终到达终结局势 的概率记作
在策略组合 σ 下,对玩家 i 而言,如下计算从根节点到当前节点的行动序列路径 h 的虚拟价值:
行动序列路径
- 经过路径 h 到达当前节点的概率 (仅考虑其他玩家策略)
- 从当前节点走到叶子结点(博弈结束)的概率 👉 终局情况
- 所到达叶子节点的收益 👉 终局收益
在定义了行动序列路径
- 当一个策略确定在信息集 I 上采取行动 a 时,就可能对"到达当前节点概率"以及"当前节点到叶子节点概率"产生影响
对能够到达同一个信息集
类似于遗憾最小化算法,虚拟遗憾最小化算法的遗憾值是
表示玩家 在第 轮中于当前节点选择行动 的遗憾值
进一步可以定义有效虚拟遗憾值:
根据有效虚拟遗憾值进行遗憾匹配以计算经过 T 轮博弈后,玩家 i 在信息集 I 情况下于后续 T + 1 轮选择行动 a 的概率:
问题描述:
- 两名玩家进行游戏博弈
- 游戏中仅提供牌值为 1、2 和 3 的三张纸牌
- 每轮中每位玩家各持一张纸牌,每位玩家根据各自的判断决定是否追加定额赌注
- 摊牌阶段比较未弃牌玩家的底牌大小,底牌值最大的玩家即为胜者
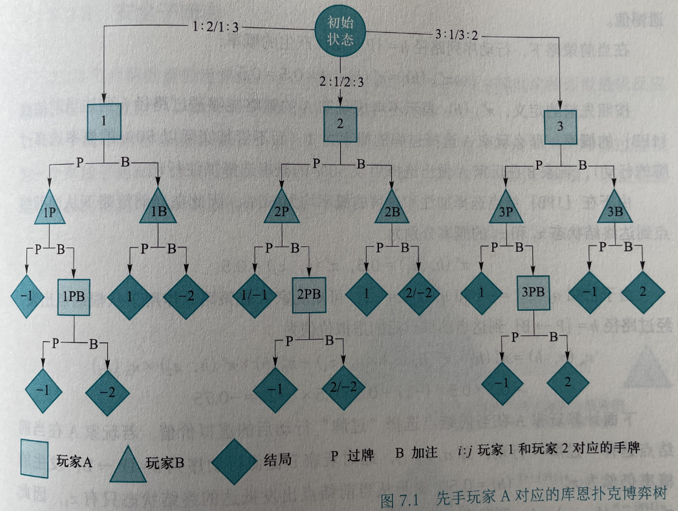
初始根结点下,三条边分别代表玩家 A 拿到三张不同手牌的情况
库恩扑克的信息集(即博弈树的中间结点)有 12 个:
在信息集中, P 表示过牌、B 表示下注
这里以信息集 {1PB} 为例, 来计算玩家 A 通过路径 1 → 1P → 1PB 到达当前节点 {1PB} 后选择“过牌”行动的遗憾值
- 在当前策略下, 行动序列路径 h = {P → B} 产生的概率:
玩家 B 在玩家 A 做出选择后以 50% 概率选择加注行动
- 当前策略下从当前节点到达终结状态
和 的概率分别为:
{1PB} 节点选择加注和过牌的概率均为 50%
- 可知玩家 A 在策略 σ 作用下从根节点出发、经过路径 h = {P → B} 到达当前节点后的虚拟价值:
已知
下面计算玩家 A 在当前节点选择“过牌”行动后的虚拟价值
- 若玩家 A 在当前节点选择“过牌”行动,即
,此时玩家 B 促使行动序列 发生的概率仍然为 - 由于从当前节点出发抵达的终结状态只有
,所以
则玩家 A 在当前节点选择“过牌”行动后的虚拟价值为:
最终,在信息集
在第一轮博弈中,累加虚拟遗憾值与行为遗憾值相同:
类似的,可以计算信息集
于是,根据遗憾值匹配算法计算结果,在下一轮的策略中会选择“过牌”策略
6.3 博弈规则设计
如何设计博弈的规则,使得博弈的最终局势能尽可能达到整体利益的最大化
双边匹配问题: 稳定婚姻问题
在给定成员偏好顺序的情况下,为两组成员寻找稳定的匹配
假设有
他们有着如下偏好:
- 对于任意一名单身男性
, 都有自己爱慕的单身女性的顺序 ,
表示第 名男性所喜欢单身女性中,排在第 位的单身女性 - 对于任意一名单身女性
也有其爱慕的单身男性顺序
表示第 名女性所喜欢单身男性中,排在第 位的单身男性 - 算法的最终目标是为这
个男士和女士匹配得到 对伴侣,每一对伴侣可以表示为
不稳定匹配:对于两对潜在的匹配伴侣
稳定匹配问题的稳定解:不存在未达成匹配的两个人都更倾向于选择对方而不是自己当前的匹配对象
- 单身男性向最喜欢的女性表白
- 所有收到表白的女性从向其表白男性中选择最喜欢的男性,暂时匹配
- 未匹配的男性继续向没有拒绝过他的女性表白。收到表白的女性如果没有完成匹配,则从这一批表白者中选择最喜欢的男性
- 即使收到表白的女性已经完成匹配,但是如果她认为有她更喜欢的男性,则可以拒绝之前的匹配者,重新匹配
- 如此循环迭代,直到所有人都成功匹配为止
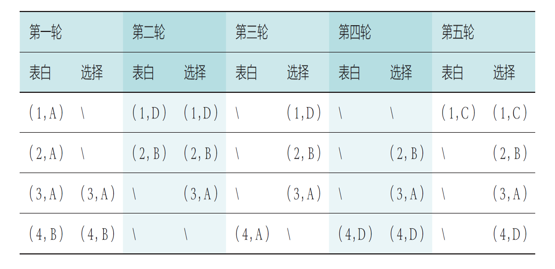
已知偏好序列:
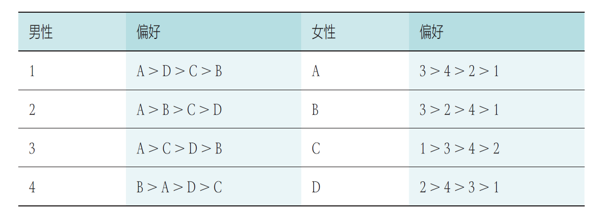
- 第一轮:4 名男性分别向自己最喜欢的女性告白,而收到 3 人告白的女性 A 选择了自己最喜欢的男性 3,另一个收到告白的女性 B 选择了男性 4
- 第二轮,尚未匹配的男性 1 和男性 2 继续向自己第二喜欢的对象告白,收到告白的女性 B 选择了自己更喜欢的男性 2 而放弃了男性 4
- 同理继续三轮告白和选择,所有人都找到了自己的伴侣,且所有匹配都是稳定的
- 可以看出,使用 G-S 算法得到了稳定匹配的结果
单边匹配问题: 最大交易圈 TTC
单边匹配问题:分配的对象都是不可分的标的物,他们只能属于一个所有者,且可以属于任何一个所有者
- 两种图节点:人节点和标的物节点,初始化可以随意分配
- 每个交易者连接一条指向他最喜欢的标的物的边,每一个标的物连接到其占有者或是具有高优先权的交易者
- 此时形成一张有向图,且必存在环,这种环被称为“交易圈”,
- 对于交易圈中的交易者,将每人指向结点所代表的标的物赋予交易者
- 交易者和标的物均离开市场
- 接着从剩余的交易者和标的物之间重复进行交易圈匹配,直到无法形成交易圈,算法停止
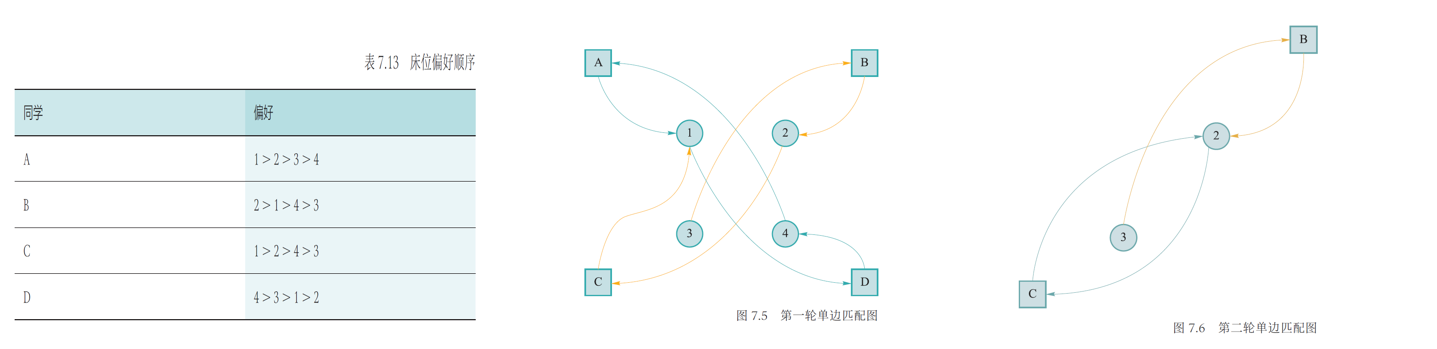
假设某寝室有 A、B、C、D 四位同学和 1、2、3、4 四个床位,当前给 A、B、C、D 四位同学随机分配 4、3、2、1 四个床位
在图 7.5 可以看出,A 和 D 之间构成一个交易圈,可达成交易,所以 A 得到床位 1,D 得到床位 4,之后将 A 和 D 以及 1 和 4 从匹配图中移除
从图 7.6 可以看出,B 和 C 都希望得到床位 2,无法再构成交易圈,但是由于 C 是床位的本身拥有者,所以 C 仍然得到床位 2,B 只能选择床位 3